Question

（本小题满分12分）

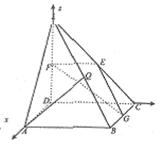
如图(1)在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD＝DC＝PD＝2，E、F、G分别是PC、PD、BC的中点，现将△PDC沿CD折起，使平面PDC⊥平面ABCD(如图2)

(1)求二面角G－EF－D的大小；

(2)在线段PB上确定一点Q，使PC⊥平面ADQ，并给出证明过程.

 

Answer 1

【答案】

(1) 45°；(2) 点Q是线段PB的中点

【解析】(1)利用向量法求解，先建系，然后求出二面角两个面的法向量，再根据法向量的夹角与二面角相等或互补来解.

（2）易证PC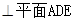,因为E为PC的中点，所以当Q为PB的中点时，PC⊥平面ADQ.也可利用向量法推证.

解：(1)建立如图所示空间直角坐标系，设平面GEF的一个法向量为n＝(x，y，z)，则

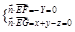  取n＝(1，0，1)      …………4分

又平面EFD的法向量为m＝(1，0，0)

∴cos<m，n> 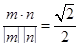＝                 …………6分

∴<m，n>＝45°                            …………7分

(2)设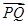＝λ (0＜λ＜1)

则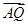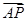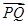＝＋＝(－2＋2λ，2λ，2－2λ)       …………9分

∵AQ⊥PC ó 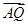·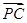＝0  ó  2×2λ－2(2－2λ)＝0

ó  λ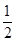＝                 …………11分

又AD⊥PC，∴PC⊥平面ADQ  ó λ＝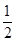

ó  点Q是线段PB的中点.                            …………12分