题目内容
已知函数 的图象过
的图象过 ,且
,且 内角A、B、C所对应边分别为a、b、c,若
内角A、B、C所对应边分别为a、b、c,若
①求 的值及
的值及 的单调递增区间
的单调递增区间
②求 的面积。
的面积。
 的图象过
的图象过 ,且
,且 内角A、B、C所对应边分别为a、b、c,若
内角A、B、C所对应边分别为a、b、c,若
①求
 的值及
的值及 的单调递增区间
的单调递增区间②求
 的面积。
的面积。⑴
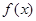 的单调递减增区间为
的单调递减增区间为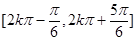
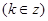 ⑵
⑵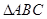 的面积为
的面积为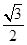 或
或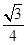

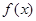 的单调递减增区间为
的单调递减增区间为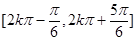
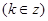 ⑵
⑵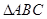 的面积为
的面积为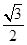 或
或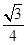
(1)由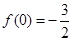 ,求出
,求出 的值,再利用三角函数的公式把
的值,再利用三角函数的公式把 化简为
化简为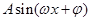 的形式,根据正弦函数的单调性求得增区间;(2)由
的形式,根据正弦函数的单调性求得增区间;(2)由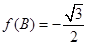 和
和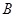 的范围,求出
的范围,求出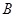 ,再根据正弦定理和面积公式可解答。
,再根据正弦定理和面积公式可解答。
⑴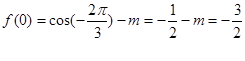

 (2分)
(2分)
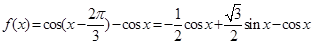
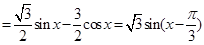

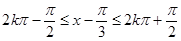
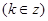

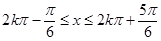
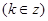

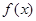 的单调递减增区间为
的单调递减增区间为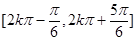
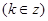 (7分)
(7分)
⑵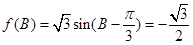

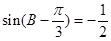
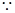
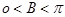

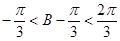

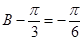

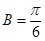
正弦定理得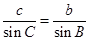

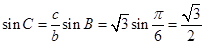
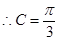 或
或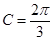 当
当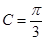 时,得
时,得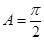 则
则 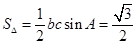
当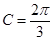 时,得
时,得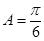 则
则 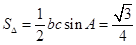

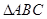 的面积为
的面积为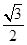 或
或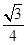
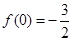 ,求出
,求出 的值,再利用三角函数的公式把
的值,再利用三角函数的公式把 化简为
化简为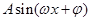 的形式,根据正弦函数的单调性求得增区间;(2)由
的形式,根据正弦函数的单调性求得增区间;(2)由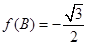 和
和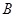 的范围,求出
的范围,求出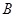 ,再根据正弦定理和面积公式可解答。
,再根据正弦定理和面积公式可解答。⑴
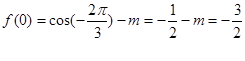

 (2分)
(2分)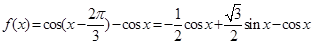
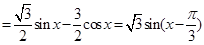

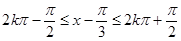
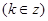

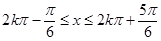
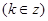

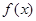 的单调递减增区间为
的单调递减增区间为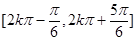
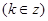 (7分)
(7分)⑵
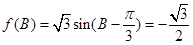

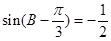
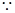
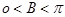

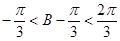

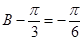

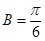
正弦定理得
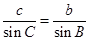

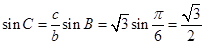
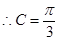 或
或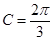 当
当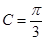 时,得
时,得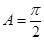 则
则 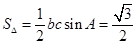
当
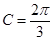 时,得
时,得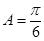 则
则 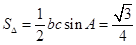

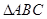 的面积为
的面积为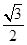 或
或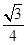

练习册系列答案
相关题目
 的部分图象如图1所示,则
的部分图象如图1所示,则 ( )
( )





 的值;
的值; 的最大值和最小值。
的最大值和最小值。 为坐标原点,向量
为坐标原点,向量 ,点
,点 是直线
是直线 上的一点,且点
上的一点,且点 分有向线段
分有向线段 的比为
的比为 .
.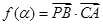 ,
, ,讨论函数
,讨论函数 的单调性,并求其值域;
的单调性,并求其值域; 三点共线,求
三点共线,求 的值.
的值.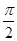 x的最小值、最大值分别是( )
x的最小值、最大值分别是( ) 1,1
1,1 (
( )的最小正周期是
)的最小正周期是 ,若其图像向右平移
,若其图像向右平移 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数 的图像
的图像 对称
对称 对称
对称 对称
对称 对称
对称
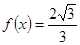 ,求sin2x的值;
,求sin2x的值;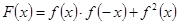 的最大值与单调递增区间.
的最大值与单调递增区间.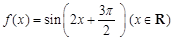 ,给出下面四个命题:①函数
,给出下面四个命题:①函数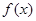 的最小正周期为
的最小正周期为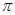 ;
;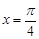 对称;④函数
对称;④函数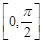 上是增函数,其中错误命题的序号是 .
上是增函数,其中错误命题的序号是 . 的周期,振幅,初相分别是( )
的周期,振幅,初相分别是( )


