题目内容
【题目】[选修4—4：坐标系与参数方程]
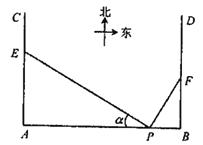
以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位．已知直线l的参数方程是
(t为参数)，圆C的极坐标方程是ρ＝4cos θ，求直线l被圆C截得的弦长．
【答案】
【解析】
由题意，消去参数即可得到直线的普通方程，利用极坐标与直角坐标的互化公式，即可得到曲线的极坐标方程，再利用圆的弦长公式，即可求解弦长.
解：直线l的参数方程
(t为参数)化为直角坐标方程是y＝x－3，
圆C的极坐标方程ρ＝4cos θ化为直角坐标方程是x2＋y2－4x＝0．
圆C的圆心(2，0)到直线x－y－3＝0的距离为d＝
＝
．
又圆C的半径r＝2，
所以直线l被圆C截得的弦长为2
＝
．
练习册系列答案
相关题目
