题目内容
二面角 的平面角是锐角,点C
的平面角是锐角,点C 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
| A.∠CEB>∠DEB | B.∠CEB=∠DEB |
| C.∠CEB<∠DEB | D.∠CEB与∠DEB的大小关系不能确定 |
A.
解析试题分析:因为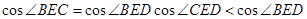 ,因为
,因为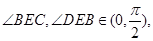
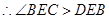 .
.
考点:二面角,线面角,余弦函数的单调性.
点评:解本小题用到了一个重要的结论:平面内的一条直线与这个平面的斜线所成的角的余弦值等于这条直线与这条斜线在这个平面内的射影所成的角的余弦值乘以斜线与平面所成的角的余弦,据此可得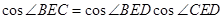 ,因为0<
,因为0<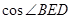 <1,所以
<1,所以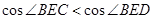 ,再利用余弦函数的单调性即可得到∠CEB>∠DEB.
,再利用余弦函数的单调性即可得到∠CEB>∠DEB.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知 ,则
,则
A. | B. | C. | D. |
设函数 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A.把 的图象向左平移 的图象向左平移 个单位,得到一个偶函数的图象 个单位,得到一个偶函数的图象 |
B. 的图象关于点 的图象关于点 对称 对称 |
C. 的图象关于直线 的图象关于直线 对称 对称 |
D. 的最小正周期为 的最小正周期为 ,且在 ,且在 上为增函数 上为增函数 |
函数 的图象的一条对称轴方程是 ( )
的图象的一条对称轴方程是 ( )
A. | B. | C. | D. |
函数 的图像与
的图像与 轴的交点的横坐标构成一个公差为
轴的交点的横坐标构成一个公差为 的等差数列,要得到函数
的等差数列,要得到函数 的图像,只需将
的图像,只需将 的图像( )
的图像( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
为了得到函数 的图象,只需把函数
的图象,只需把函数 的图象( )
的图象( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移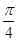 个长度单位 个长度单位 | D.向右平移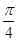 个长度单位 个长度单位 |
如图,为了得到这个函数的图象,只要将 的图象上所有的点( )
的图象上所有的点( )
A.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
B.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
 为第四象限角,
为第四象限角, ,则
,则 =
=
A. | B. | C. | D. |
把函数y=sin(x+ )图像上各点的横坐标缩短为原来的
)图像上各点的横坐标缩短为原来的 倍(纵坐标不变),再将图像向右平移
倍(纵坐标不变),再将图像向右平移 个单位,那么所得图像的一条对称轴方程为
个单位,那么所得图像的一条对称轴方程为
A.x=- | B.x =- |
C.x = | D.x = |