��Ŀ����
����Ŀ����ͼ��ij����С����һ���������й㳡��AB=20�ף��㳡��һ���ǰ뾶Ϊ16������BCE�̻�����Ϊ��ʹС�������ܹ����õ��ڹ㳡���з��ɣ��־����ڹ㳡�ϰ������������Σ�����һ���Ǵ�Խ�㳡��˫�˿���ֱ����MN�����Ȳ��ƣ�����M���߶�AD�ϣ�����������CE���У���һ��Ϊ���˻�����������CN�����Ȳ��ƣ��ڷţ���֪˫�˿���ֱ���ε����ÿ��Ϊ2aԪ�����˻����ε����ÿ��ΪaԪ������ǡ�NBE=�ȣ������ΪWԪ�� 
��1���Խ�W��ʾΪ�ȵĺ���W���ȣ�����д��cos�ȵ�ȡֵ��Χ��
��2�����ѡȡ��M��λ�ã���ʹ�����W��С��
���𰸡�
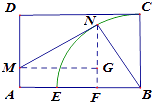
��1���⣺��N��AB�Ĵ��ߣ�����ΪF����M��NF�Ĵ��ߣ�����ΪG��
��Rt��BNF�У�BF=16cos�ȣ���MG=20��16cos��
��Rt��MNG�� ![]() ��
��
�������� ![]() ��
��
��ˣ� ![]() ��
�� ![]()
��2���⣺ ![]()
��W�䣨�ȣ�=0�� ![]() ����Ϊ
����Ϊ ![]() ������
������ ![]() ��
��
����Ǧ�1���� ![]() ��
�� ![]()
�� ![]() ʱ��W�����ȣ���0��W���ȣ������ݼ���
ʱ��W�����ȣ���0��W���ȣ������ݼ���
�� ![]() ʱ��W�����ȣ���0��W���ȣ�����������
ʱ��W�����ȣ���0��W���ȣ�����������
���Ե� ![]() �������W��С����СֵΪ
�������W��С����СֵΪ ![]() ��
��
��ʱ ![]() ��
�� ![]() ��
�� ![]() ��
��
��˵� ![]() ��ʱ����ʹ�������С
��ʱ����ʹ�������С
����������1����N��AB�Ĵ��ߣ�����ΪF����M��NF�Ĵ��ߣ�����ΪG������ֱ�������Σ�ͨ����ֱ�������Ρ����ɶ����ͻ�����ʽ���н�𣻣�2������1���еĺ�����ϵ���б��εõ� ![]() ��W�䣨�ȣ�=0��
��W�䣨�ȣ�=0�� ![]() ����Ϊ
����Ϊ ![]() ������
������ ![]() ��Ȼ���Ϧȵ�ȡֵ��Χ���з������ۣ��������Ǻ����ĵ����Խ��н��
��Ȼ���Ϧȵ�ȡֵ��Χ���з������ۣ��������Ǻ����ĵ����Խ��н��
�����㾫�����������Ǻ�������ֵ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����![]() ����
����![]() ʱ��ȡ����СֵΪ
ʱ��ȡ����СֵΪ![]() ����
����![]() ʱ��ȡ�����ֵΪ
ʱ��ȡ�����ֵΪ![]() ����
����![]() ��
��![]() ��
��![]() ��
��

 �߽�������ϵ�д�
�߽�������ϵ�д�
