题目内容
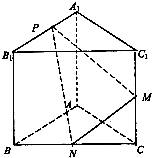 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=l,AB⊥AC,M是CC1的中点,N是BC的中点,K是AC中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=l,AB⊥AC,M是CC1的中点,N是BC的中点,K是AC中点,点P在直线A1B1上,且满足| A1P |
| A1B1 |
(Ⅰ)求证:PN⊥AM;
(Ⅱ)求三棱锥P-MNK的体积.
分析:(Ⅰ)通过证明AB⊥平面ACC1A1,说明AB⊥AM,证明AM⊥NK,然后证明AM⊥平面A1KNP,即可求证:PN⊥AM;
(Ⅱ)通过AB∥NK,所以A1B1∥NK,则P到平面MNK的距离是定值,利用四面体体积不变,转化顶点是方法,采用等体积求三棱锥P-MNK的体积.
(Ⅱ)通过AB∥NK,所以A1B1∥NK,则P到平面MNK的距离是定值,利用四面体体积不变,转化顶点是方法,采用等体积求三棱锥P-MNK的体积.
解答:解:(Ⅰ)因为AC中点为K,则N,K,A1,P四点在一个平面内,
由于AA1⊥平面ABC,所以AA1⊥AB,又AB⊥AC,所以AB⊥平面ACC1A1,所以AB⊥AM,
所以AB⊥AM,又AB∥NK,所以AM⊥NK,
在正方形中,利用相似可知AM⊥A1K,
故AM⊥平面A1KNP,
所以PN⊥AM;
(Ⅱ)因为K是AC的中点,所以AB∥NK,所以A1B1∥NK,则P到平面MNK的距离是定值,等于A1到MNK的距离,
三棱锥P-MNK的体积与三棱锥N-MA1K的体积相等.有(1)知AB⊥平面ACC1A1,N到平面ACC1A1,的距离为
AB=
,
MA1K的面积为:1-2×
×1×
-
×
×
=
,
所以三棱锥N-MA1K的体积为:
×
×
=
,
所求棱锥的体积为:
.
由于AA1⊥平面ABC,所以AA1⊥AB,又AB⊥AC,所以AB⊥平面ACC1A1,所以AB⊥AM,
所以AB⊥AM,又AB∥NK,所以AM⊥NK,
在正方形中,利用相似可知AM⊥A1K,
故AM⊥平面A1KNP,
所以PN⊥AM;
(Ⅱ)因为K是AC的中点,所以AB∥NK,所以A1B1∥NK,则P到平面MNK的距离是定值,等于A1到MNK的距离,
三棱锥P-MNK的体积与三棱锥N-MA1K的体积相等.有(1)知AB⊥平面ACC1A1,N到平面ACC1A1,的距离为
| 1 |
| 2 |
| 1 |
| 2 |
MA1K的面积为:1-2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
所以三棱锥N-MA1K的体积为:
| 1 |
| 3 |
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 16 |
所求棱锥的体积为:
| 1 |
| 16 |
点评:本题考查直线与平面垂直的判定定理以及性质定理的应用,几何体的体积的求法,考查空间想象能力与转化思想的应用.

练习册系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4, 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则| 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.