题目内容
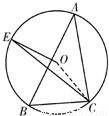
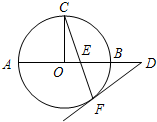
A.选修4-1:几何证明选讲锐角三角形ABC内接于⊙O,∠ABC=60?,∠BAC=40?,作OE⊥AB交劣弧
 于点E,连接EC,求∠OEC.
于点E,连接EC,求∠OEC.B.选修4-2:矩阵与变换
曲线C1=x2+2y2=1在矩阵M=[
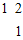 ]的作用下变换为曲线C2,求C2的方程.
]的作用下变换为曲线C2,求C2的方程.C.选修4-4:坐标系与参数方程
P为曲线C1:
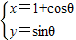 (θ为参数)上一点,求它到直线C2:
(θ为参数)上一点,求它到直线C2: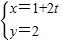 (t为参数)距离的最小值.
(t为参数)距离的最小值.D.选修4-5:不等式选讲
设n∈N*,求证:
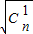 +
+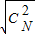 +L+
+L+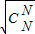 ≤
≤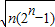 .
.
【答案】分析:A.先连OC.由∠ABC=60°,∠BAC=40°,得出∠ACB=80°从而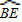 和
和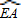 的度数均为80°.故有∠EOC=80°+80°=160°最后得出:∠OEC的大小即可;
的度数均为80°.故有∠EOC=80°+80°=160°最后得出:∠OEC的大小即可;
B.设P(x,y)为曲线C2上任意一点,P′(x′,y′)为曲线x2+4xy+2y2=1上与P对应的点,根据矩阵变换得出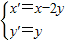 结合P′是曲线C1上的点,求得C2的方程即可;
结合P′是曲线C1上的点,求得C2的方程即可;
C.将曲线C1化成普通方程(x-1)2+y2=1,圆心是(1,0),直线C2化成普通方程最后求出曲线C1上点到直线的距离即可;
D.由柯西不等式,得:(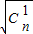 +
+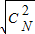 +…+
+…+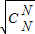 )2≤(1+1+…+1)(Cn1+Cn2+…Cn2+)=n(2n-1)即可得到证明.
)2≤(1+1+…+1)(Cn1+Cn2+…Cn2+)=n(2n-1)即可得到证明.
解答:A.选修4-1:几何证明选讲
解:连OC.∵∠ABC=60°,∠BAC=40°,∴∠ACB=80°.(4分)
∵OE⊥AB,∴E为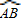 的中点,∴
的中点,∴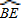 和
和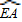 的度数均为80°.
的度数均为80°.
∴∠EOC=80°+80°=160°.(8分)
∴∠OEC=10°.(10分)
B.选修4-2:矩阵与变换
解:设P(x,y)为曲线C2上任意一点,P′(x′,y′)为曲线C2上与P对应的点,
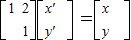 ,
,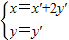 ∴
∴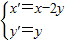 (5分)
(5分)
∵P′是曲线C1上的点,∴C2的方程(x-2y)2+y2=1.(10分)
C.选修4-4:坐标系与参数方程
解:将曲线C1化成普通方程(x-1)2+y2=1,圆心是(1,0),
直线C2化成普通方程是y-2=0,则圆心到直线的距离为2.(5分)
∴曲线C1上点到直线的距离为1,该点为(1,1).(10分)
D.选修4-5:不等式选讲
证明:由柯西不等式,得:
(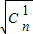 +
+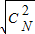 +…+
+…+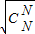 )2≤(1+1+…+1)(Cn1+Cn2+…Cn2+)=n(2n-1)
)2≤(1+1+…+1)(Cn1+Cn2+…Cn2+)=n(2n-1)
∴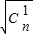 +
+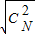 +…+
+…+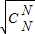 ≤
≤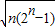 .
.
点评:本题考查柯西不等式,点到直线的距离公式、弦长公式的应用,几种特殊的矩阵变换,体现了数形结合的数学思想.
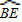 和
和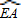 的度数均为80°.故有∠EOC=80°+80°=160°最后得出:∠OEC的大小即可;
的度数均为80°.故有∠EOC=80°+80°=160°最后得出:∠OEC的大小即可;B.设P(x,y)为曲线C2上任意一点,P′(x′,y′)为曲线x2+4xy+2y2=1上与P对应的点,根据矩阵变换得出
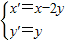 结合P′是曲线C1上的点,求得C2的方程即可;
结合P′是曲线C1上的点,求得C2的方程即可;C.将曲线C1化成普通方程(x-1)2+y2=1,圆心是(1,0),直线C2化成普通方程最后求出曲线C1上点到直线的距离即可;
D.由柯西不等式,得:(
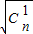 +
+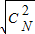 +…+
+…+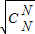 )2≤(1+1+…+1)(Cn1+Cn2+…Cn2+)=n(2n-1)即可得到证明.
)2≤(1+1+…+1)(Cn1+Cn2+…Cn2+)=n(2n-1)即可得到证明.解答:A.选修4-1:几何证明选讲
解:连OC.∵∠ABC=60°,∠BAC=40°,∴∠ACB=80°.(4分)
∵OE⊥AB,∴E为
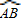 的中点,∴
的中点,∴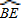 和
和 的度数均为80°.
的度数均为80°.∴∠EOC=80°+80°=160°.(8分)
∴∠OEC=10°.(10分)
B.选修4-2:矩阵与变换
解:设P(x,y)为曲线C2上任意一点,P′(x′,y′)为曲线C2上与P对应的点,
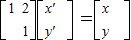 ,
,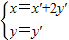 ∴
∴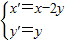 (5分)
(5分)∵P′是曲线C1上的点,∴C2的方程(x-2y)2+y2=1.(10分)
C.选修4-4:坐标系与参数方程
解:将曲线C1化成普通方程(x-1)2+y2=1,圆心是(1,0),
直线C2化成普通方程是y-2=0,则圆心到直线的距离为2.(5分)
∴曲线C1上点到直线的距离为1,该点为(1,1).(10分)
D.选修4-5:不等式选讲
证明:由柯西不等式,得:
(
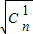 +
+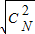 +…+
+…+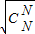 )2≤(1+1+…+1)(Cn1+Cn2+…Cn2+)=n(2n-1)
)2≤(1+1+…+1)(Cn1+Cn2+…Cn2+)=n(2n-1)∴
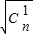 +
+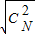 +…+
+…+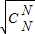 ≤
≤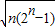 .
.点评:本题考查柯西不等式,点到直线的距离公式、弦长公式的应用,几种特殊的矩阵变换,体现了数形结合的数学思想.

练习册系列答案
相关题目
 A(选修4-1:几何证明选讲)
A(选修4-1:几何证明选讲) 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. A)选修4-1:几何证明选讲
A)选修4-1:几何证明选讲 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分. 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)