题目内容
【题目】如图,![]() 与
与![]() 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)![]() ,(2)
,(2)![]()
【解析】
解法一:(1)等体积法.
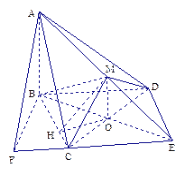
取CD中点O,连OB,OM,则OB=OM=![]() ,OB⊥CD,MO⊥CD.
,OB⊥CD,MO⊥CD.
又平面![]() 平面
平面![]() ,则MO⊥平面
,则MO⊥平面![]() ,所以MO∥AB,MO∥平面ABC.M、O到平面ABC的距离相等.
,所以MO∥AB,MO∥平面ABC.M、O到平面ABC的距离相等.
作OH⊥BC于H,连MH,则MH⊥BC.
求得OH=OC![]()
![]() ,
,
MH=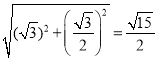 .
.
设点![]() 到平面
到平面![]() 的距离为d,由
的距离为d,由![]() 得
得![]() .
.
即![]() ,
,
解得![]() .
.
(2)延长AM、BO相交于E,连CE、DE,CE是平面![]() 与平面
与平面![]() 的交线.
的交线.
由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为![]() .
.
因为∠BCE=120°,所以∠BCF=60°.
![]() ,
,
![]() ,
,![]() .
.
则所求二面角的正弦值为![]()
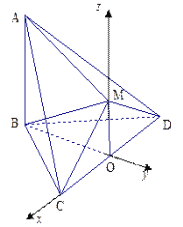
解法二:取CD中点O,连OB,OM,则
OB⊥CD,OM⊥CD.又平面![]() 平面
平面![]() ,则MO⊥平面
,则MO⊥平面![]() .
.
取O为原点,直线OC、BO、OM为x轴、y轴、z轴,建立空间直角坐标系如图.OB=OM=![]() ,则各点坐标分别为C(1,0,0),M(0,0,
,则各点坐标分别为C(1,0,0),M(0,0,![]() ),B(0,
),B(0,![]() ,0),A(0,-
,0),A(0,-![]() ,
,![]() ).
).
(1)设![]() 是平面MBC的法向量,则
是平面MBC的法向量,则![]() ,
,![]() .
.
由![]() 得
得![]() ;
;
由![]() 得
得![]() .
.
取![]() .
.![]() ,则
,则
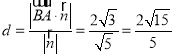 .
.
(2)![]() ,
,![]() .
.
设平面ACM的法向量为![]() ,由
,由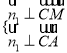 得
得 解得
解得![]() ,
,![]() ,取
,取![]() .又平面BCD的法向量为
.又平面BCD的法向量为![]() .
.
所以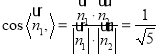 ,
,
设所求二面角为![]() ,则
,则![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: ,
,![]() .
.
【题目】某种植物感染![]() 病毒极易导致死亡,某生物研究所为此推出了一种抗
病毒极易导致死亡,某生物研究所为此推出了一种抗![]() 病毒的制剂,现对20株感染了
病毒的制剂,现对20株感染了![]() 病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:mg)进行统计.规定:植株吸收在6mg(包括6mg)以上为“足量”,否则为“不足量”.现对该20株植株样本进行统计,其中 “植株存活”的13株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:mg)进行统计.规定:植株吸收在6mg(包括6mg)以上为“足量”,否则为“不足量”.现对该20株植株样本进行统计,其中 “植株存活”的13株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量(mg) | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成以下![]() 列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关?
列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关?
吸收足量 | 吸收不足量 | 合计 | |
植株存活 | 1 | ||
植株死亡 | |||
合计 | 20 |
(2)①若在该样本“吸收不足量”的植株中随机抽取3株,记![]() 为“植株死亡”的数量,求
为“植株死亡”的数量,求![]() 得分布列和期望
得分布列和期望![]() ;
;
②将频率视为概率,现在对已知某块种植了1000株并感染了![]() 病毒的该植物试验田里进行该药品喷雾试验,设“植株存活”且“吸收足量”的数量为随机变量
病毒的该植物试验田里进行该药品喷雾试验,设“植株存活”且“吸收足量”的数量为随机变量![]() ,求
,求![]() .
.
参考数据: ,其中
,其中![]()