[题目]已知圆的方程为x2+y2﹣6x=0.过点(1.2)的该圆的三条弦的长a1 . a2 . a3构成等差数列.则数列a1 . a2 . a3的公差的最大值是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知圆的方程为x2+y2﹣6x=0，过点（1，2）的该圆的三条弦的长a1 ， a2 ， a3构成等差数列，则数列a1 ， a2 ， a3的公差的最大值是．

【答案】2
【解析】解：如图，由x2+y2﹣6x=0，得（x﹣3）2+y2=9，

∴圆心坐标C（3，0），半径r=3，

由圆的性质可知，过点P（1，2）的该圆的弦的最大值为圆的直径，等于6，

最小值为过P且垂直于CP的弦的弦长，

∵|CP|= ，

∴|AB|=2 ，

即a1=2，a3=6，

∴公差d的最大值为．

故答案为：2．

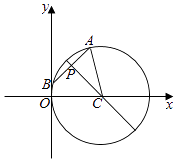
化圆的一般方程为标准方程，求出圆心坐标和半径，得到最大弦长，再求出过P且垂直于CP的弦的弦长，即最小弦长，然后利用等差数列的通项公式求得公差得答案．

练习册系列答案

【题目】已知两条直线m，n和两个不同平面α，β，满足α⊥β，α∩β=l，m∥α，n⊥β，则（）
A.m∥n
B.m⊥n
C.m∥l
D.n⊥l

【题目】在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的半圆分别交BA及其延长线于点M，N，点P在上运动（如图）．若，其中λ，μ∈R，则2λ﹣5μ的取值范围是（）
A.[﹣2，2]
B.
C.
D.

【题目】已知函数f（x）=alnx+b（a，b∈R），曲线f（x）在x=1处的切线方程为x﹣y﹣1=0．
（Ⅰ）求a，b的值；
（Ⅱ）证明：；
（Ⅲ）已知满足xlnx=1的常数为k．令函数g（x）=mex+f（x）（其中e是自然对数的底数，e=2.71828…），若x=x0是g（x）的极值点，且g（x）≤0恒成立，求实数m的取值范围．

【题目】已知m≠0，向量 =（m，3m），向量 =（m+1，6），集合A={x|（x﹣m2）（x+m﹣2）=0}．
（1）判断“ ∥ ”是“| |= ”的什么条件
（2）设命题p：若 ⊥ ，则m=﹣19，命题q：若集合A的子集个数为2，则m=1，判断p∨q，p∧q，￢q的真假，并说明理由．

【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且满足acosB=bcosA．
（1）判断△ABC的形状；
（2）求sin（2A+ ）﹣2cos2B的取值范围．

【题目】秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x的值为2，则输出的v值为（）
A.9×210﹣2
B.9×210+2
C.9×211+2
D.9×211﹣2

【题目】在直角坐标系xOy中，曲线C1的参数方程为（φ为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=4sinθ
（Ⅰ）求曲线C1的普通方程和C2的直角坐标方程；
（Ⅱ）已知曲线C3的极坐标方程为θ=α，0＜α＜π，ρ∈R，点A是曲线C3与C1的交点，点B是曲线C3与C2的交点，且A，B均异于原点O，且|AB|=4 ，求实数a的值．

试题分类