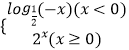题目内容
【题目】在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的半圆分别交BA及其延长线于点M，N，点P在 
上运动（如图）．若 
，其中λ，μ∈R，则2λ﹣5μ的取值范围是（ ） 
A.[﹣2，2]
B.
C.
D.
【答案】C
【解析】解：建立如图所示的坐标系，
则A（0，0），B（2，0），D（0，1），C（2，2），E（2，1），F（1，1.5），
P（cosα，sinα）（0≤α≤π），
由 
=λ 
+μ 
得，（cosα，sinα）=λ（2，1）+μ（﹣1， 
）
cosα=2λ﹣μ，sinα=λ+ 
λ= 
， 
∴2λ﹣5μ=2（ ）﹣5（ 
）
=﹣2（sinα﹣cosα）=﹣2 
sin（ 
）
∵ ∈[﹣ 
， 
]∴﹣2 sin（ ）∈[﹣2 ，2]，
即2λ﹣5μ的取值范围是[﹣2 ，2]．
故选：C
【考点精析】通过灵活运用平面向量的基本定理及其意义，掌握如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
即可以解答此题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
