题目内容
已知不等式ax +bx+1<0的解集为{x|-1<x<2},则ab=
+bx+1<0的解集为{x|-1<x<2},则ab=
 +bx+1<0的解集为{x|-1<x<2},则ab=
+bx+1<0的解集为{x|-1<x<2},则ab=| A.-1 | B.- | C.-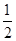 | D.1 |
B
试题分析:将不等式的解集问题转化为对应的方程根的问题,再利用韦达定理,即可求得结论。根据题意,由于不等式ax
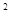 +bx+1<0的解集为{x|-1<x<2},那么可知-1和2是方程ax
+bx+1<0的解集为{x|-1<x<2},那么可知-1和2是方程ax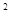 +bx+1=0的来两个实数根,那么根据韦达定理可知,
+bx+1=0的来两个实数根,那么根据韦达定理可知,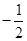 =a,b=-a=
=a,b=-a=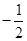 ,那么可知ab=-
,那么可知ab=-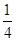 ,故答案为B
,故答案为B点评:本题主要考查一元二次不等式与一元二次方程解之间的关系,解题的关键是利用韦达定理,易错点是忽视a<0,而引起增解

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
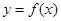 的图象.写出
的图象.写出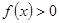 的解集;
的解集;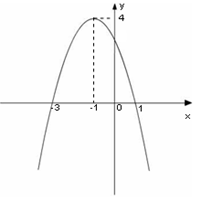
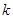 在何范围内变化时,
在何范围内变化时,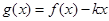 在区间
在区间 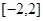 上是单调函数.
上是单调函数.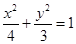 的左右焦点分别为
的左右焦点分别为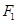 、
、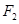 ,点
,点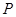 是椭圆上任意一点,则
是椭圆上任意一点,则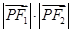 的取值范围是( )
的取值范围是( )



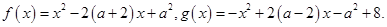 设
设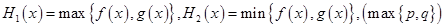 表示
表示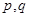 中的较大值,
中的较大值,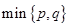 表示
表示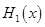 得最小值为
得最小值为
 得最小值为
得最小值为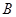 ,则
,则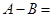




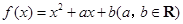 的值域为
的值域为 ,若关于x的不等式
,若关于x的不等式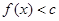 的解集为
的解集为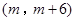 ,则实数c的值为 .
,则实数c的值为 . 、
、 的图象
的图象 、
、 相交于点P(-2,3),则不等式
相交于点P(-2,3),则不等式 <
< 的解集是 .
的解集是 .
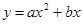 与指数函数
与指数函数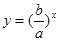 在同一坐标系中的图象可能是
在同一坐标系中的图象可能是