Question

【题目】已知AB是⊙O的直径，直线AF交⊙O于F（不与B重合），直线EC与⊙O相切于C，交AB于E，连接AC，且∠OAC=∠CAF，求证：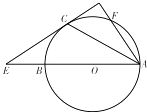

（1）AF⊥EC；
（2）若AE=5，AF=2，求AC．

Answer 1

【答案】
（1）证明：设EC与AF交于M，连接BC，则BC⊥AC，

因为直线EC与⊙O相切于C，

所以∠ACM=∠ABC，

因为∠OAC=∠CAF，

所以∠OAC+∠ABC=∠CAF+∠ACM=90°，

所以AF⊥EC

（2）解：连接CF，则∠MCF=∠MAC，∠ECB=∠OAC，

因为∠OAC=∠CAF，

所以∠ACE=∠AFC，

所以△ACE∽△AFC，

所以 ，

所以AC2=AEAF，

因为AE=5，AF=2，

所以AC= ．

【解析】（1）设EC与AF交于M，连接BC，则BC⊥AC，证明∠OAC+∠ABC=∠CAF+∠ACM=90°，即可证明AF⊥EC；（2）证明△ACE∽△AFC，可得AC2=AEAF，利用AE=5，AF=2，求AC．