题目内容
8.已知函数f(x)=x-1-lnx(1)求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)求函数f(x)的极值.
分析 (1)求函数的导数,利用导数的几何意义即可曲线y=f(x)在点(2,f(2))处的切线方程;
(2)求函数的导数,根据函数极值和导数之间的关系即可求函数f(x)的极值.
解答 解:(1)函数的定义域为(0,+∞),
函数的f(x)的导数f′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$,
则f′(2)=$\frac{2-1}{2}$=$\frac{1}{2}$,f(2)=2-1-ln2=1-ln2,
则曲线y=f(x)在点(2,f(2))处的切线方程为y-(1-ln2)=$\frac{1}{2}$(x-2),
即y=(1-ln2)+$\frac{1}{2}$(x-2)=$\frac{1}{2}$x-ln2;
(2)∵f′(x)=$\frac{x-1}{x}$,
∴由f′(x)>0得x>1,此时函数递增,
由f′(x)<0得0<x<1,此时函数递减,
故当x=1时,函数取得极大值f(1)=1-1-ln1=0,无极小值.
点评 本题主要考查函数切线的求解,以及函数极值的求解,利用导数的应用是解决本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
1.函数h(x)=2sin(2x+$\frac{π}{6}$),函数f(x)=2cos(2x-$\frac{2π}{3}$)可由h(x)经过( )的变换得到.
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
2.已知复数z=$\frac{1-2i}{3+4i}$(i是虚数单位),则z的共轭复数的虚部是( )
| A. | -$\frac{2}{5}$i | B. | $\frac{2}{5}$i | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
17.如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆α千克,则共需油漆的总量为( )
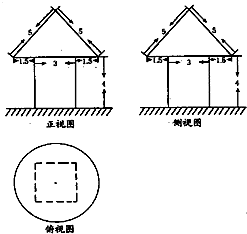

| A. | (48+36π)α千克 | B. | (39+24π)α千克 | C. | (36+36π)α千克 | D. | (36+30π)α千克 |
18.${({\frac{1+i}{1-i}})^{2015}}$=( )
| A. | i | B. | -1 | C. | 1 | D. | -i |