题目内容
(本小题满分13分)
已知椭圆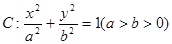 经过点(p,q),离心率
经过点(p,q),离心率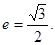 其中p,q分别表示标准正态分布的期望值与标准差。
其中p,q分别表示标准正态分布的期望值与标准差。
(1)求椭圆C的方程;
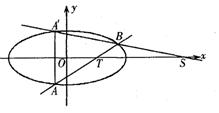
(2)设直线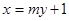 与椭圆C交于A,B两点,点A关于x轴的对称点为
与椭圆C交于A,B两点,点A关于x轴的对称点为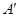
 。①试建立
。①试建立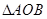 的面积关于m的函数关系;②莆田十中高三(1)班数学兴趣小组通过试验操作初步推断:“当m变化时,直线
的面积关于m的函数关系;②莆田十中高三(1)班数学兴趣小组通过试验操作初步推断:“当m变化时,直线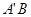 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
【答案】
解:(1)依题意椭圆过点(0,1),从而可得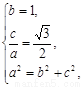 …………2分
…………2分
解得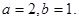 …………3分
…………3分
所以椭圆C的方程是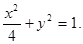 …………4分
…………4分
(2)①由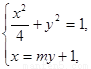
得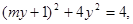 即
即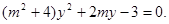 …………5分
…………5分
记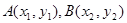
则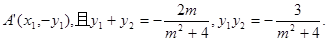 ………6分
易求S=
………6分
易求S=
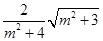
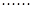 8分
②
8分
②
特别地,令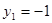 ,则
,则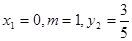
此时 ,直线
,直线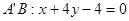 与x轴的交点为S(4,0)
与x轴的交点为S(4,0)
若直线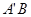 与x轴交于一个定点,则定点只能为S(4,0) …………9分
与x轴交于一个定点,则定点只能为S(4,0) …………9分
以下证明对于任意的m,直线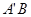 与x轴交于定点S(4,0)
与x轴交于定点S(4,0)
事实上,经过点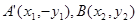 的直线方程为
的直线方程为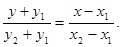
令y=0,得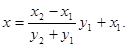
只需证明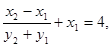 …………11分
…………11分
即证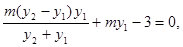
即证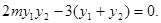
因为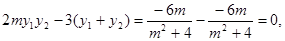
所以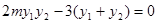 成立。
成立。
这说明,当m变化时,直线 与x轴交于点S(4,0) …………13分
与x轴交于点S(4,0) …………13分
【解析】略

练习册系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和