题目内容
13.绵阳市某高中的5名高三学生计划在高考结束后到北京、上海、杭州、广州等4个城市去旅游,要求每个城市都要有学生去,每个学生只去一个城市旅游,且学生甲不到北京,则不同的出行安排有( )| A. | 180种 | B. | 72种 | C. | 216种 | D. | 204种 |
分析 先安排甲,再安排其余4人,利用分步计算原理可得结论.
解答 解:甲在上海、杭州、广州中任选一个,有3种方法,在这个前提下,剩下4个人可以到北京、上海、杭州、广州等4个城市种各一个城市,就是${A}_{4}^{4}$=24,也可以在除了甲去的之外的3个城市旅游,就是${C}_{4}^{2}{A}_{3}^{3}$=36,
∴不同的安排方案共有3(24+36)=180.
故选:A.
点评 本题考查分步计算原理的运用,考查学生的计算能力,属于基础题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
4.某几何体的三视图如图所示,其中俯视图为正三角形,则该几何体的表面积为( )

| A. | 10 | B. | 10+$\sqrt{3}$ | C. | 12+$\sqrt{2}$ | D. | 12+$\sqrt{3}$ |
8.曲线y=2axlnx在x=$\frac{1}{{e}^{2}}$(e为自然对数的底数)处的切线与直线2x+y+1=0垂直,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
5.函数f(x)=sin(2x+$\frac{π}{3}$)的一个单调递增区间是( )
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [-$\frac{π}{2}$,0] | C. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | D. | [$\frac{π}{12}$,$\frac{7π}{12}$] |
2.复数z=$\frac{1}{1-i}+\frac{a}{1+i}$(a∈R,i为虚数单位)在复平面上对应的点不可能位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
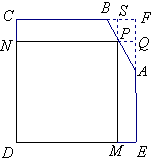 有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2.
有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2.  执行如图所示的程序框图,输出的结果为a,二项式${({\sqrt{m}{x^2}+\frac{1}{{\sqrt{x}}}})^4}$的展开式中x3项的系数为$\frac{a}{2}$,则常数m=$\frac{1}{4}$.
执行如图所示的程序框图,输出的结果为a,二项式${({\sqrt{m}{x^2}+\frac{1}{{\sqrt{x}}}})^4}$的展开式中x3项的系数为$\frac{a}{2}$,则常数m=$\frac{1}{4}$.