题目内容
4.(1)已知a,b都是正数,且a≠b,求证:a3+b3>a2b+ab2;(2)已知a,b,c都是正数,求证:$\frac{{{a^2}{b^2}+{b^2}{c^2}+{c^2}{a^2}}}{a+b+c}$≥abc.
分析 (1)由条件a≠b推出:a2-2ab+b2>0,通过变形,应用不等式的性质可证出结论;
(2)利用基本不等式,再相加,即可证明结论.
解答 证明:(1)∵a≠b,∴a-b≠0,∴a2-2ab+b2>0,∴a2-ab+b2>ab.
而a,b均为正数,∴a+b>0,∴(a+b)(a2-ab+b2)>ab(a+b)
∴a3+b3>a2b+ab2 成立;
(2)∵a,b,c都是正数,
∴a2b2+b2c2≥2acb2,a2b2+c2a2≥2bca2,c2a2+b2c2≥2abc2,
三式相加可得2(a2b2+b2c2+c2a2)≥2abc(a+b+c),
∴a2b2+b2c2+c2a2)≥abc(a+b+c),
∴$\frac{{{a^2}{b^2}+{b^2}{c^2}+{c^2}{a^2}}}{a+b+c}$≥abc.
点评 本题考查不等式的证明,考查基本不等式的运用,考查综合法,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.设实数x,y满足$\left\{\begin{array}{l}{y≤3}\\{x-y-2≤0}\\{3x-2y-6≥0}\end{array}\right.$则$\frac{y-2}{x-y}$的取值范围为( )
| A. | [$\frac{1}{2}$,1] | B. | (-∞,-1]∪[1,+∞) | C. | [-1,1] | D. | [-1,$\frac{1}{2}$] |
9.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-2≤0}\\{y≥-3}\end{array}\right.$,则目标函数z=x-y的最大值( )
| A. | -2 | B. | 2 | C. | 4 | D. | 8 |
13.已知cosα=k,k∈R,α∈($\frac{π}{2}$,π),则sin(π+α)=( )
| A. | -$\sqrt{1-{k}^{2}}$ | B. | $\sqrt{1-{k}^{2}}$ | C. | ±$\sqrt{1-{k}^{2}}$ | D. | -k |
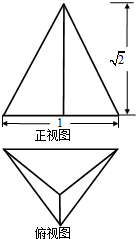 已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为$\frac{\sqrt{6}}{4}$.
已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为$\frac{\sqrt{6}}{4}$.