题目内容
若关于x的方程
=kx2有四个不同的实数解，则实数k的取值范围是
| |x| |
| x+4 |
(
，+∞)
| 1 |
| 4 |
(
，+∞)
．| 1 |
| 4 |
分析：分x=0和x≠0分析方程解的情况，x=0方程显然成立，不等于0时消掉x后利用数形结合的方法画图分析．
解答：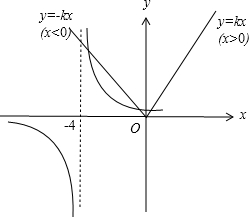
解：方程
=kx2有四个不同的实数解，
x=0是方程的1个根，
当x≠0时方程变为k|x|=
①．
要使方程①有3个不为0的实数根，
则函数y=k|x|和y=
应有3个不同的交点，
如图，
k＜0显然不成立，当k＞0时y=kx（x＞0）与y=
有一个交点，
只需y=-kx（x＜0）和y=
有两个交点即可，
联立
，得kx2+4kx+1=0．
由△=（4k）2-4k=0，得k=
．
∴k＞
时y=-kx（x＜0）和y=
有两个交点．
综上，关于x的方程
=kx2有四个不同的实数解的实数k的取值范围是(
，+∞)．
故答案为：（
，+∞）．
解：方程| |x| |
| x+4 |
x=0是方程的1个根，
当x≠0时方程变为k|x|=
| 1 |
| x+4 |
要使方程①有3个不为0的实数根，
则函数y=k|x|和y=
| 1 |
| x+4 |
如图，
k＜0显然不成立，当k＞0时y=kx（x＞0）与y=
| 1 |
| x+4 |
只需y=-kx（x＜0）和y=
| 1 |
| x+4 |
联立
|
由△=（4k）2-4k=0，得k=
| 1 |
| 4 |
∴k＞
| 1 |
| 4 |
| 1 |
| x+4 |
综上，关于x的方程
| |x| |
| x+4 |
| 1 |
| 4 |
故答案为：（
| 1 |
| 4 |
点评：本题考查了根的存在性与根的个数的判断，考查了数形结合及分类讨论的数学思想方法，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
若关于x的方程ax+2x-4=0（a＞0且a≠1）的所有根记作x1，x2，…，xm（m∈N*），关于x的方程loga2x+x-2=0的所有根记作x1′，x2′，…，xn′（n∈N*），则
的值为（ ）
x1+x2+…+xm+
| ||||||
| m+n |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
若关于x的方程x|x-a|=a有三个不相同的实根，则实数a的取值范围为（ ）
| A、（0，4） | B、（-4，0） | C、（-∞，-4）∪（4，+∞） | D、（-4，0）∪（0，4） |