Question

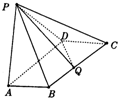如图，四棱锥P-ABCD中，底面ABCD是矩形，AB=

3

，BC=a，又PA⊥平面ABCD，PA=4．
（Ⅰ）若在边BC上存在一点Q，使PQ⊥QD，求a的取值范围；
（Ⅱ）若a=4，且PQ⊥QD，求二面角A-PD-Q的大小．

Answer 1

分析：（Ⅰ）在边BC上存在一点Q，使PQ⊥QD，则PQ²+QD²=PD²，从而可得方程，利用判别式大于等于0，可求a的取值范围；
（Ⅱ）因为面PAD⊥面ABCD，所以过Q作 QM⊥AD，则QM⊥面PAD，过M作MN⊥PD，由三垂线定理有QN⊥PD，从而∠MNQ是二面角A-PD-Q的平面角，再在△MNQ中，利用正切函数可求．

解答：解：（Ⅰ）设BQ=t，AQ²=3+t²，则
PQ²=19+t²，QD²=3+（a-t）²，PD²=16+a²
由PQ⊥QD得：19+t²+3+（a-t）²=16+a²，即t²-at+3=0
∴△=a²-12≥0⇒a≥2

3

．
（Ⅱ）由（Ⅱ）得当a=4时，t²-4t+3=0，t=1或t=3
因为面PAD⊥面ABCD，
所以过Q作 QM⊥AD，则QM⊥面PAD，
过M作MN⊥PD，由三垂线定理有QN⊥PD
所以∠MNQ是二面角A-PD-Q的平面角
在Rt△PAD中，

MN

PA

=

MD

PD

⇒MN=

4-t

2

，
当t=1时，tan∠MNQ=

3

3 2

=

6

3

当t=3时，tan∠MNQ=

3

1 2

=

6

∴二面角A-PD-Q的大小为arctan

6

3

或arctan

6

．

点评：本题以线面垂直为载体，考查线线垂直，考查面面角，关键是正确作出面面角．