题目内容
设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+(a2-5)=0},
(1)若A∩B={2},求实数a值;
(2)若A∪B=A,求实数a的取值范围。
(1)若A∩B={2},求实数a值;
(2)若A∪B=A,求实数a的取值范围。
解:(1)A={1,2},
∵A∩B={2},
∴2∈B,
∴ ,∴a=-1或-3,
,∴a=-1或-3,
经检验,a=-1或-3符合题意,
∴a=-1或a=-3。
(2)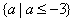 。
。
∵A∩B={2},
∴2∈B,
∴
 ,∴a=-1或-3,
,∴a=-1或-3,经检验,a=-1或-3符合题意,
∴a=-1或a=-3。
(2)
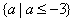 。
。
练习册系列答案
相关题目