题目内容
（2013•成都二模）设G为△ABC的重心，若△ABC所在平面内一点P满足
+2
+2
=
，则
的值等于
| PA |
| BP |
| CP |
| 0 |
|
| ||
|
|
2
2
．分析：利用向量的基本运算将条件足
+2
+2
=
，化简转化为共线关系，然后根据长度确定比值即可．
| PA |
| BP |
| CP |
| 0 |
解答：解：由足
+2
+2
=
，得
=-2
-2
=2(
+
)，
设AC的中点为M，则
+
=2
，
所以
=4
，所以|
|=4|
|，
又因为G为△ABC的重心，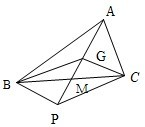
所以G为PA的中点，
所以
=2．
故答案为：2．
| PA |
| BP |
| CP |
| 0 |
| PA |
| BP |
| CP |
| PB |
| PC |
设AC的中点为M，则
| PB |
| PC |
| PM |
所以
| PA |
| PM |
| PA |
| PM |
又因为G为△ABC的重心，
所以G为PA的中点，
所以
|
| ||
|
|
故答案为：2．
点评：本题主要考查向量的共线定理的应用，属于中档题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
（2013•成都二模）一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的体积为（ ）