题目内容
(2013•成都二模)在平面直角坐标系xOy中,已知点A(l,2),若P是拋物线 y2=2x上一动点,则P到y轴的距离与P到点A的距离之和的最小值为( )
分析:根据题意算出抛物线的焦点为F(
,0),准线l方程为x=-
.设点P在y轴上的射影为Q点,延长PQ交准线l于点B,连结PF,根据抛物线的定义得|PQ|+|PA|=|PB|+|PA|-
=|PF|+|PA|-
,再由|PF|+|PA|≥|AF|得当P、A、F三点共线时,|PQ|+|PA|取得最小值,结合坐标系内两点间的距离公式,即可得P到y轴的距离与P到点A的距离之和的最小值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: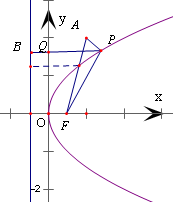 ∵拋物线的方程为 y2=2x,
∵拋物线的方程为 y2=2x,
∴抛物线的焦点为F(
,0),准线l方程为x=-
设点P在y轴上的射影为Q点,延长PQ交准线l于点B,连结PF
则PQ长即为点P到y轴的距离,可得|PB|=|PQ|+
,
根据抛物线的定义,得|PB|=|PF|
∴|PQ|+|PA|=|PB|+|PA|-
=|PF|+|PA|-
,
根据平面几何知识,可得|PF|+|PA|≥|AF|,得|PQ|+|PA|≥|AF|-
.
当且仅当P、A、F三点共线时等号成立
∵|AF|=
=
-
=
∴当P、A、F三点共线时,|PQ|+|PA|的最小值为
即P到y轴的距离与P到点A的距离之和的最小值为
故选:D
 ∵拋物线的方程为 y2=2x,
∵拋物线的方程为 y2=2x,∴抛物线的焦点为F(
| 1 |
| 2 |
| 1 |
| 2 |
设点P在y轴上的射影为Q点,延长PQ交准线l于点B,连结PF
则PQ长即为点P到y轴的距离,可得|PB|=|PQ|+
| 1 |
| 2 |
根据抛物线的定义,得|PB|=|PF|
∴|PQ|+|PA|=|PB|+|PA|-
| 1 |
| 2 |
| 1 |
| 2 |
根据平面几何知识,可得|PF|+|PA|≥|AF|,得|PQ|+|PA|≥|AF|-
| 1 |
| 2 |
当且仅当P、A、F三点共线时等号成立
∵|AF|=
(1-
|
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴当P、A、F三点共线时,|PQ|+|PA|的最小值为
| ||
| 2 |
即P到y轴的距离与P到点A的距离之和的最小值为
| ||
| 2 |
故选:D
点评:本题给出抛物线上动点P和定点A(1,2),求P到y轴的距离与P到点A的距离之和的最小值.着重考查了抛物线的定义与标准方程和抛物线的简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
 (2013•成都二模)一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( )
(2013•成都二模)一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( )