题目内容
(本 小题满分12分)在△ABC中, a, b, c分别为角A, B, C所对的边,
小题满分12分)在△ABC中, a, b, c分别为角A, B, C所对的边,
且4sin2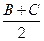 -cos2A=
-cos2A=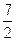 .
.
(1)求角A的度数; (2)若a=
(2)若a=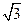 , b+c=3,求b和c的值.
, b+c=3,求b和c的值.
 小题满分12分)在△ABC中, a, b, c分别为角A, B, C所对的边,
小题满分12分)在△ABC中, a, b, c分别为角A, B, C所对的边,且4sin2
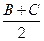 -cos2A=
-cos2A=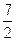 .
.(1)求角A的度数;
 (2)若a=
(2)若a=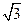 , b+c=3,求b和c的值.
, b+c=3,求b和c的值.解:(1)由题设 得2[1-cos(B+C)]-(2cos2A-1)=
得2[1-cos(B+C)]-(2cos2A-1)=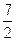 ,
,
∵ cos(B+C)=-cosA,∴ 2(1+cosA)-2cos2A+1=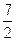 ,
,
整理得(2cosA-1)2=0,∴ cosA=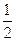 ,∴ A=60°.
,∴ A=60°.
( 2)∵ cosA=
2)∵ cosA= =
=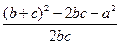 =
= =
=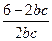
∴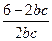 =
=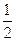 ,∴ bc=2. 又∵ b+c=3,∴ b=1, c=2或b=2,
,∴ bc=2. 又∵ b+c=3,∴ b=1, c=2或b=2, c=1.
c=1.
 得2[1-cos(B+C)]-(2cos2A-1)=
得2[1-cos(B+C)]-(2cos2A-1)=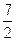 ,
,∵ cos(B+C)=-cosA,∴ 2(1+cosA)-2cos2A+1=
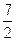 ,
,整理得(2cosA-1)2=0,∴ cosA=
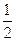 ,∴ A=60°.
,∴ A=60°.(
 2)∵ cosA=
2)∵ cosA= =
=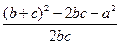 =
= =
=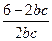
∴
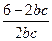 =
=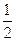 ,∴ bc=2. 又∵ b+c=3,∴ b=1, c=2或b=2,
,∴ bc=2. 又∵ b+c=3,∴ b=1, c=2或b=2, c=1.
c=1.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
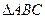 中,
中,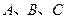 的对边分别为
的对边分别为
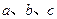 ,且
,且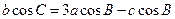 .
. 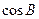 的值;
的值;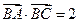 ,
,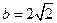 ,求
,求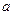 和
和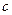 .
.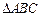 中, a,b,c分别是A、B、C的对边,且
中, a,b,c分别是A、B、C的对边,且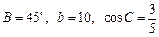 .
. 中,若
中,若 ,则
,则 的范围( )
的范围( )



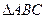 中,
中,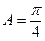 ,
,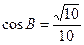 .
.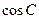 ;
;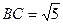 ,求
,求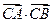 的值.
的值. 中,
中,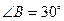 ,
,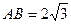 ,
,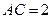 ,求
,求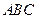 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为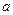 、
、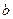 、
、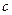 .且
.且 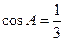 .
.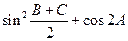 的值;
的值;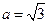 ,求
,求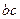 的最大值.
的最大值.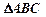 的三个内角
的三个内角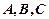 所对的边分别为
所对的边分别为
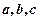 ,若
,若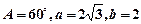 ,
,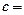 .
.