题目内容
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
当过点M(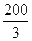 ,
,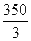 ),利润总额z=900x+600y取最大值130000元.
),利润总额z=900x+600y取最大值130000元.
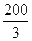 ,
,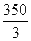 ),利润总额z=900x+600y取最大值130000元.
),利润总额z=900x+600y取最大值130000元. 试题分析:解:设生产甲、乙两种棉纱分别为x、y吨,利润总额为z,
则z=900x+600y 2
且
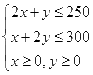 4
4作出以上不等式组所表示的平面区域(如图),
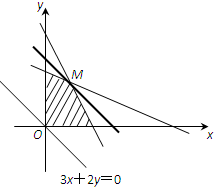
即可行域. 6
作直线l:900x+600y=0,即3x+2y=0,
把直线l向右上方平移至过直线2x+y=250与
直线x+2y=300的交点位置M(
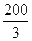 ,
,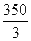 ), 10
), 10此时所求利润总额z=900x+600y取最大值130000元. 12
点评:主要是考查了线性规划的最优解的运用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为9,则
的最大值为9,则
 的最小值为__ ___.
的最小值为__ ___. 满足约束条件
满足约束条件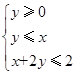 ,则
,则 的最大值为____________.
的最大值为____________. , 若目标函数z=ax+by(a>0,b>0)的最大值为12,则
, 若目标函数z=ax+by(a>0,b>0)的最大值为12,则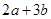 的值为
的值为 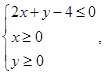 则
则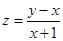 的取值范围是 。
的取值范围是 。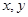 满足约束条件
满足约束条件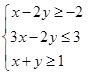 ,若
,若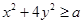 恒成立,则实数
恒成立,则实数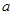 的最大值为( )
的最大值为( )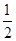
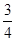
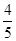
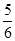
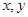 满足约束条件
满足约束条件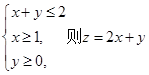 的最大值和最小值分别为( )
的最大值和最小值分别为( )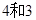
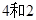
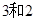

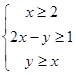 ,若目标函数
,若目标函数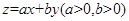 的最小值为2,则ab的最大值( )
的最小值为2,则ab的最大值( )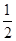
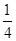
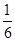
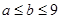 ,②
,②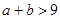 ,则同时满足①②的正整数
,则同时满足①②的正整数 有 组.
有 组.