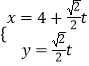题目内容
【题目】如图，在梯形ABCD中，AB∥CD，AD＝DC＝CB＝1，∠BCD＝120°，四边形BFED为矩形，平面BFED⊥平面ABCD，BF＝1．
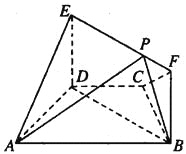
（1）求证：AD⊥平面BFED；
（2）已知点P在线段EF上，
＝2．求三棱锥E－APD的体积．
【答案】（1）证明详见解析；（2）
.
【解析】
试题分析: 本题主要考查线面垂直的判定与性质、空间几何体体积等基础知识，考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、计算能力. 第一问，在
中，利用余弦定理计算出
的值，可以看出，
符合勾股定理，得到
，再由面面垂直的性质定理得线面垂直，从而得
，最后由线面垂直的判定定理得到结论；第二问，由线面垂直的性质得
即
是锥体的高，用等体积转化法将
转化为
，用体积公式计算.
试题解析：（1）在梯形
中，
∵
∥
，
∴
∴
∴
∴
∵平面
平面
平面
平面
，
∴
∴
又
∴
（2）由（1）知⊥平面
∵//
, ∴且
∴
练习册系列答案
阅读快车系列答案
相关题目
【题目】某食品店为了了解气温对销售量的影响，随机记录了该店1月份中5天的日销售量
（单位：千克）与该地当日最低气温
（单位： 
）的数据，如下表：
| 2 | 5 | 8 | 9 | 11 |
| 12 | 10 | 8 | 8 | 7 |
（1）求出
与
的回归方程
；
（2）判断
与
之间是正相关还是负相关；若该地1月份某天的最低气温为6
，请用所求回归方程预测该店当日的营业额.
附: 回归方程
中，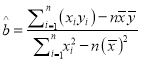 
,
