题目内容
已知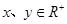 ,且
,且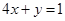 ,求
,求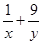 的最小值.某同学做如下解答:
的最小值.某同学做如下解答:
因为 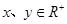 ,所以
,所以 ┄①,
┄①, ┄②,
┄②,
①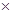 ②得
②得 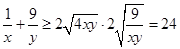 ,所以
,所以 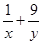 的最小值为24.
的最小值为24.
判断该同学解答是否正确,若不正确,请在以下空格内填写正确的最小值;若正确,请在以下空格内填写取得最小值时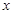 、
、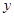 的值. .
的值. .
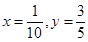 .
.
解析试题分析:本题考查基本不等式的应用,注意应用基本不等式求最大(小)值时的条件:“一正”,“二定”,“三相等”.表面上看,本题不等式的推理过程没有错误,但仔细观察,应该能发现①式等号成立的条件是 ,②式等号成立的条件是
,②式等号成立的条件是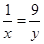 ,两式中等号成立的条件不相同,因此最后的最小值24是不能取得的,正确的方法应该是
,两式中等号成立的条件不相同,因此最后的最小值24是不能取得的,正确的方法应该是 ,当且仅当
,当且仅当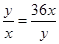 ,即
,即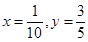 时,等号成立,故最小值为25.
时,等号成立,故最小值为25.
考点:基本不等式的应用.

练习册系列答案
相关题目
 时,
时, 的最小值是 .
的最小值是 .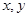 均为正实数,且
均为正实数,且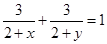 ,则
,则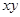 的最小值为 .
的最小值为 .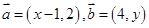 ,若
,若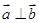 ,则
,则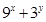 的最小值为 .
的最小值为 . ,若
,若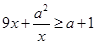 对一切正实数
对一切正实数 成立,则
成立,则 的取值范围为_________.
的取值范围为_________. 、
、 满足
满足 ,则当
,则当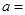 ______时,
______时, 取得最小值.
取得最小值.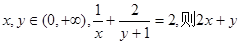 的最小值为 。
的最小值为 。 的图象交于P,Q两点,则线段PQ长的最小值是 .
的图象交于P,Q两点,则线段PQ长的最小值是 .
 +
+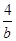 的最小值为________.
的最小值为________.