题目内容
(2010•浙江模拟)设函数f(x)=2cos2x+2
sinxcosx+m(x∈R)
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若x∈[0,
],是否存在实数m,使函数f(x)的值域恰为[
,
]?若存在,请求出m的取值;若不存在,请说明理由.
| 3 |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若x∈[0,
| π |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
分析:(I)由题意可得:f(x)=2sin(2x+
)+m+1,再结合周期的计算公式可得答案.
(Ⅱ)假设存在实数m符合题意,由x的范围得:
≤2x+
≤
,进而求出函数f(x)的范围,再结合题意可得答案.
| π |
| 6 |
(Ⅱ)假设存在实数m符合题意,由x的范围得:
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
解答:解:(I)由题意可得:
f(x)=2cos2x+2
sinxcosx+m
=1+cos2x+
sin2x+m
=2sin(2x+
)+m+1,
所以函数f(x)的最小正周期T=
=π.
(Ⅱ)假设存在实数m符合题意,∵x∈[0,
],
∴
≤2x+
≤
,则sin(2x+
)∈[-
,1]…(9分)
∴f(x)=2sin(2x+
)+m+1∈[m,3+m]…(10分)
又∵f(x)∈[
,
],解得 m=
…(13分)
∴存在实数m=
,使函数f(x)的值域恰为[
,
]…(14分)
f(x)=2cos2x+2
| 3 |
=1+cos2x+
| 3 |
=2sin(2x+
| π |
| 6 |
所以函数f(x)的最小正周期T=
| 2π |
| 2 |
(Ⅱ)假设存在实数m符合题意,∵x∈[0,
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴f(x)=2sin(2x+
| π |
| 6 |
又∵f(x)∈[
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
∴存在实数m=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
点评:本题题考查三角函数的周期性及其求法,以及三角函数的有关性质,两角和与差的正弦函数,二倍角公式,并且考查计算能力,是中档题型.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
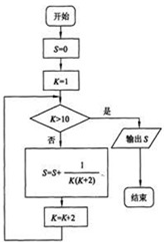 (2010•浙江模拟)若某一程序框图如图所示,则该程序运行后输出的S等于
(2010•浙江模拟)若某一程序框图如图所示,则该程序运行后输出的S等于 (2010•浙江模拟)已知四棱锥P-ABCD,底面是边长为1的正方形,侧棱PC长为2,且PC⊥底面ABCD,E是侧棱PC上的动点.
(2010•浙江模拟)已知四棱锥P-ABCD,底面是边长为1的正方形,侧棱PC长为2,且PC⊥底面ABCD,E是侧棱PC上的动点.