题目内容
【题目】已知抛物线![]() 的焦点为F,过F的直线与抛物线交于A,B两点,点O为坐标原点,则下列命题中正确的个数为( )
的焦点为F,过F的直线与抛物线交于A,B两点,点O为坐标原点,则下列命题中正确的个数为( )
①![]() 面积的最小值为4;
面积的最小值为4;
②以![]() 为直径的圆与x轴相切;
为直径的圆与x轴相切;
③记![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④过焦点F作y轴的垂线与直线![]() ,
,![]() 分别交于点M,N,则以
分别交于点M,N,则以![]() 为直径的圆恒过定点.
为直径的圆恒过定点.
A.1B.2C.3D.4
【答案】C
【解析】
依次判断每个选项:![]() 的斜率为0时,
的斜率为0时,![]() ,所以①错误,计算
,所以①错误,计算![]() ②正确,证明
②正确,证明![]() ,所以③正确,根据等式令
,所以③正确,根据等式令![]() ,得
,得![]() 或3,所以④正确,得到答案.
或3,所以④正确,得到答案.
当![]() 的斜率为0时,
的斜率为0时,![]() ,所以①错误.
,所以①错误.
设![]() 的中点为E,作
的中点为E,作![]() 轴交x轴于点G,作
轴交x轴于点G,作![]() 准线交准线于点D,交x轴于点C,则
准线交准线于点D,交x轴于点C,则![]() ,又
,又![]() ,
,
所以![]() ,所以②正确.
,所以②正确.
直线![]() 的方程为
的方程为![]() ,联立
,联立![]() ,得
,得![]() .设
.设![]() ,
,![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,所以③正确.
,所以③正确.
直线![]() ,所以
,所以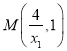 .同理可得
.同理可得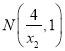 .所以以
.所以以![]() 为直径的圆的方程为
为直径的圆的方程为 ,即
,即![]() .
.
令![]() ,得
,得![]() 或3,所以④正确.
或3,所以④正确.
故选:![]() .
.


练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目