题目内容
若数列{an}满足a1=2且an+an-1=2n+2n-1,Sn为数列{an}的前n项和,则log2(S2012+2)等于( )
| A.2013 | B.2012 | C.2011 | D.2010 |
A
由题意得a2+a1=22+2,a4+a3=24+23,a6+a5=26+25,…,a2012+a2011=22012+22011,
以上1006个等式相加得
S2012=2+22+23+…+22012=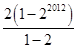 =2(22012-1)=22013-2.
=2(22012-1)=22013-2.
故log2(S2012+2)=log2(22013-2+2)=2013.
以上1006个等式相加得
S2012=2+22+23+…+22012=
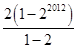 =2(22012-1)=22013-2.
=2(22012-1)=22013-2.故log2(S2012+2)=log2(22013-2+2)=2013.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
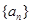 ,其前
,其前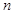 项和
项和 满足
满足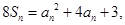 且
且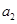 是
是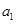 和
和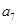 的等比中项..
的等比中项..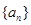 的通项公式;
的通项公式;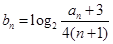 ,求数列
,求数列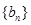 的前99项和.
的前99项和.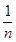 )2an(n∈N*),则数列{an}的通项公式为 .
)2an(n∈N*),则数列{an}的通项公式为 .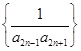 的前n项和.
的前n项和.