题目内容
棱长为2的正四面体ABCD在空间直角坐标系中移动,但保持点A,B分别在x轴、y轴上移动,则原点O到直线CD的最近距离为
-1
-1.
| 2 |
| 2 |
分析:固定正四面体ABCD的位置,则原点O在以AB为直径的球面上运动,所以原点O到直线CD的最近距离为点M到直线CD的距离减去球M的半径,求解即可.
解答: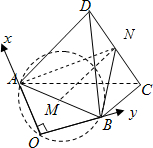 解:如图,若固定正四面体ABCD的位置,则原点O在以AB为直径的球面上运动,
解:如图,若固定正四面体ABCD的位置,则原点O在以AB为直径的球面上运动,
设AB中点为M,则原点到直线CD的最近距离d等于点M到直线CD的距离减去球M的半径,
NB=
,MB=1,所以MN=
,
所求距离的最小值为:d=
.
故答案为:
-1.
 解:如图,若固定正四面体ABCD的位置,则原点O在以AB为直径的球面上运动,
解:如图,若固定正四面体ABCD的位置,则原点O在以AB为直径的球面上运动,设AB中点为M,则原点到直线CD的最近距离d等于点M到直线CD的距离减去球M的半径,
NB=
| 3 |
| 2 |
所求距离的最小值为:d=
| 2-1 |
故答案为:
| 2 |
点评:本题考查空间想象能力,转化思想的应用,考查分析问题解决问题的能力与计算能力.

练习册系列答案
相关题目
棱长为
的正四面体的外接球的体积为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )



