题目内容
如图,四面体 的三条棱
的三条棱 两两垂直,
两两垂直, ,
, ,
,
为四面体 外一点.给出下列命题.
外一点.给出下列命题.

①不存在点 ,使四面体
,使四面体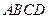 有三个面是直角三角形;
有三个面是直角三角形;
②不存在点 ,使四面体
,使四面体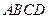 是正三棱锥;
是正三棱锥;
③存在点 ,使
,使 与
与 垂直并且相等;
垂直并且相等;
④存在无数个点 ,使点
,使点 在四面体
在四面体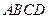 的外接球面上.
的外接球面上.
其中真命题的序号是 .
 的三条棱
的三条棱 两两垂直,
两两垂直, ,
, ,
,
为四面体
 外一点.给出下列命题.
外一点.给出下列命题.
①不存在点
 ,使四面体
,使四面体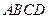 有三个面是直角三角形;
有三个面是直角三角形;②不存在点
 ,使四面体
,使四面体 是正三棱锥;
是正三棱锥;③存在点
 ,使
,使 与
与 垂直并且相等;
垂直并且相等;④存在无数个点
 ,使点
,使点 在四面体
在四面体 的外接球面上.
的外接球面上.其中真命题的序号是 .
③④
略

练习册系列答案
相关题目
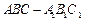 ,
,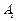 在底面ABC上的射影恰为AC的中点D,
在底面ABC上的射影恰为AC的中点D,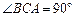 ,
, ,又知
,又知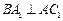
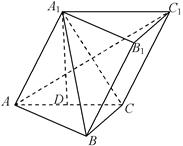
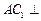 平面
平面
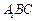 ;
;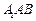 的距离;
的距离;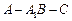 余弦值的大小.
余弦值的大小.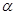 ,那么对于空间内的任意一条直线
,那么对于空间内的任意一条直线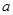 ,在平面
,在平面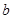 ,使得
,使得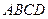 中,
中,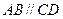 ,
,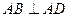 ,且
,且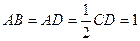 .
.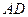 为一边向形外作正方形
为一边向形外作正方形 ,然后沿边
,然后沿边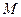 为
为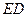 的中点,如图2.
的中点,如图2.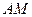 ∥平面
∥平面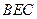 ;
;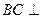 平面
平面 ;
; 到平面
到平面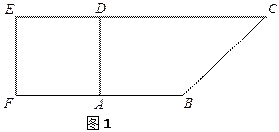
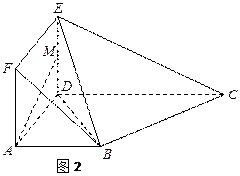
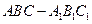 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
,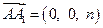 ,其中
,其中 、
、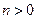

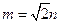 ,求直线
,求直线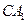 与平面
与平面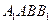 所成角的大小。
所成角的大小。 n作为点P的坐标
n作为点P的坐标 ,求:
,求:
 上的概率;
上的概率; 外的概率.
外的概率.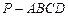 中,底面
中,底面 是平行四边形,
是平行四边形,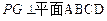 ,垂足为
,垂足为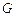 ,
,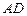 上,且
上,且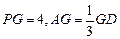 ,
,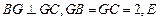 是
是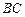 的中点.
的中点.
 与
与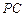 所成的角的余弦值;
所成的角的余弦值;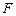 是棱
是棱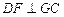 ,求
,求 的值.
的值.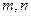 是两不同的直线,
是两不同的直线, 是两不同的平面,则下列命题正确的是 ( )
是两不同的平面,则下列命题正确的是 ( )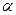 ⊥
⊥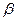 ,
,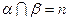 ,
,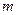 ⊥
⊥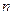 ,则
,则
 棱PA="PD" =
棱PA="PD" =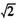 ,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.
,底面 ABCD为直角梯形,其中BC//AD,AB丄AD,AD=2AB=2BC=2,0为AD中点.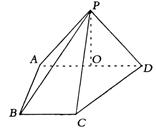
 PCD的距离.
PCD的距离.