题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知椭圆![]() 的方程为
的方程为![]() ,
,![]() 、
、![]() 和
和![]() 为
为![]() 的三个顶点.
的三个顶点.
(1)若点![]() 满足
满足![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .若
.若![]() ,证明:
,证明:![]() 为
为![]() 的中点;
的中点;
(3)设点![]() 在椭圆
在椭圆![]() 内且不在
内且不在![]() 轴上,如何构作过
轴上,如何构作过![]() 中点
中点![]() 的直线
的直线![]() ,使得
,使得![]() 与椭圆
与椭圆![]() 的两个交点
的两个交点![]() 、
、![]() 满足
满足![]()
![]() ?令
?令![]() ,
,![]() ,点
,点![]() 的坐标是(-8,-1),若椭圆
的坐标是(-8,-1),若椭圆![]() 上的点
上的点![]() 、
、![]() 满足
满足![]() ,求点
,求点![]() 、
、![]() 的坐标.
的坐标.
解析:(1) ![]() ;
;
(2) 由方程组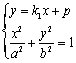 ,消y得方程
,消y得方程![]() ,
,
因为直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,
两点,
所以D>0,即![]() ,
,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则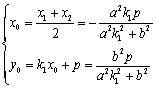 ,
,
由方程组![]() ,消y得方程(k2-k1)x=p,
,消y得方程(k2-k1)x=p,
又因为![]() ,所以
,所以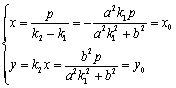 ,
,
故E为CD的中点;
(3) 因为点P在椭圆Γ内且不在x轴上,所以点F在椭圆Γ内,可以求得直线OF的斜率k2,由![]() 知F为P1P2的中点,根据(2)可得直线l的斜率
知F为P1P2的中点,根据(2)可得直线l的斜率![]() ,从而得直线l的方程.
,从而得直线l的方程.
![]() ,直线OF的斜率
,直线OF的斜率![]() ,直线l的斜率
,直线l的斜率![]() ,
,
解方程组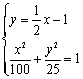 ,消y:x2-2x-48=0,解得P1(-6,-4)、P2(8,3).
,消y:x2-2x-48=0,解得P1(-6,-4)、P2(8,3).

练习册系列答案
相关题目
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处