题目内容
已知函数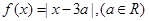
(1)当a=1时,解不等式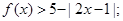
(2)若存在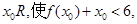 成立,求a的取值范围.
成立,求a的取值范围.
(1)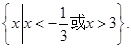 (2)
(2) .
.
解析试题分析:(1)当 时,原不等式等价于
时,原不等式等价于 ,可采用零点分段法解不等式,即分成
,可采用零点分段法解不等式,即分成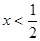 ,
, ,
, 三种情况去绝对值,分别解不等式,最后求并集;属于基础题型;
三种情况去绝对值,分别解不等式,最后求并集;属于基础题型;
(2)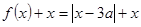 ,分
,分 和
和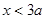 两种情况去绝对值,得到分段函数,得到函数的最小值为
两种情况去绝对值,得到分段函数,得到函数的最小值为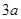 ,若存在
,若存在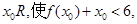 成立,只需
成立,只需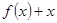 的最小值小于6,得到
的最小值小于6,得到 的取值范围,此问属于比较简单的恒成立问题.
的取值范围,此问属于比较简单的恒成立问题.
(1)当 时,不等式
时,不等式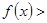
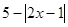 可化为
可化为 ,
,
当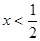 时,不等式即
时,不等式即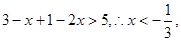
当 时,不等式即
时,不等式即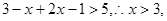 所以
所以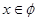 ,
,
当 时,不等式即
时,不等式即 ,
,
综上所述不等式的解集为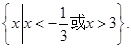 5分
5分
(2)令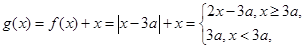
所以函数 最小值为
最小值为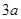 ,
,
根据题意可得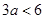 ,即
,即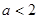 ,所以
,所以 的取值范围为
的取值范围为 . 10分
. 10分
考点:1.解不等式;2.恒成立问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
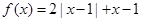 ,
,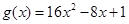 ,记
,记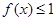 的解集为M,
的解集为M,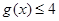 的解集为N.
的解集为N.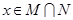 时,证明:
时,证明: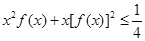 .
.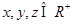 ,求证
,求证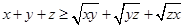 ;
; ,求证:
,求证: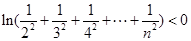 .
. 、
、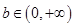 ,
,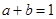 ,求
,求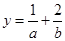 的最小值.
的最小值.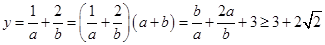 ,
,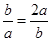 ,即
,即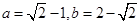 时取到等号,
时取到等号,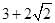 .
.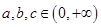 ,
,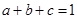 ,求
,求 的最小值;
的最小值;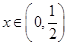 ,求函数
,求函数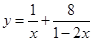 的最小值;
的最小值;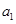 、
、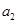 、
、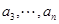 ,
,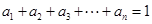 ,
,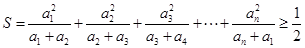 .
.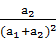 +
+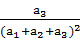 +…+
+…+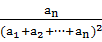 <
< .
. ,
,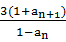 =
= ,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=
,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=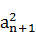 -
-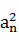 (n≥1,n∈N+).
(n≥1,n∈N+). 的最小值.
的最小值.