题目内容
证明下列不等式:
(1)已知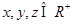 ,求证
,求证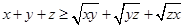 ;
;
(2) ,求证:
,求证: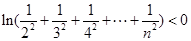 .
.
(1)证明详见解析;(2)证明详见解析.
解析试题分析:(1)本小题主要考查基本不等式 ,
, (当且仅当
(当且仅当 时等号成立)的应用问题,分别得到
时等号成立)的应用问题,分别得到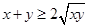 、
、 、
、 ,进而再利用同向不等式的可加性即可得到结论;(2)本小问,主要考查放缩法与裂项求和法.先由
,进而再利用同向不等式的可加性即可得到结论;(2)本小问,主要考查放缩法与裂项求和法.先由 得到
得到 ,进而裂项求和得到
,进而裂项求和得到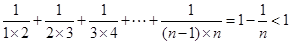 ,从而问题得证.
,从而问题得证.
(1) 证明:
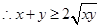 (当且仅当
(当且仅当 时等号成立),
时等号成立), (当且仅当
(当且仅当 时等号成立),
时等号成立), ,(当且仅当
,(当且仅当 时等号成立) 3分
时等号成立) 3分
三个不等式相加可得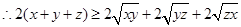 即
即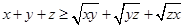 6分
6分
(2)因为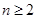 时,
时,
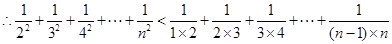
又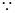

 9分
9分
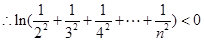 12分.
12分.
考点:1.基本不等式的应用;2.不等式的证明——放缩法;3.裂项求和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ≥1的实数解为________.
≥1的实数解为________. .
. 的解集为空集,求
的解集为空集,求 的范围;
的范围; ,且
,且 ,求证:
,求证: .
.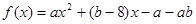 ,当
,当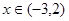 时,
时,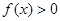 ;
;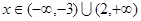 时,
时,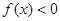 。
。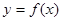 的解析式
的解析式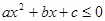
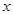 的不等式
的不等式 .
.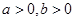 ,且
,且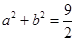 ,若
,若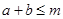 恒成立.
恒成立.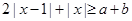 对任意的
对任意的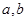 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.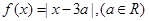
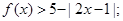
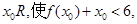 成立,求a的取值范围.
成立,求a的取值范围.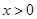 ,
,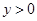 ,
,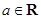 ,
,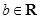 .求证
.求证 .
.