题目内容
选修4-2:矩阵与变换已知矩阵M=
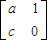 的一个特征值为-l,属于它的一个特征向量
的一个特征值为-l,属于它的一个特征向量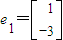 .
.(1)求矩阵M;
(2)若点P(1,1)经过矩阵M所对应的变换得到点Q,求点Q的坐标.
【答案】分析:(1)利用特征值、特征向量的定义,构建方程组,由此可求矩阵M.
(2)根据二阶矩阵与列向量乘法的定义即可求解点Q的坐标.
解答:解:(1)由题知,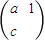
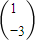 =
= ,
,
即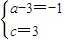 ,
,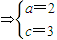
∴M=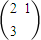 ,
,
(2)∴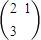
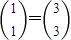 ,即点Q的坐标(3,3).
,即点Q的坐标(3,3).
点评:本题考查待定系数法求矩阵,考查特征值与特征向量,理解特征值、特征向量的定义是关键.
(2)根据二阶矩阵与列向量乘法的定义即可求解点Q的坐标.
解答:解:(1)由题知,
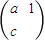
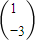 =
= ,
,即
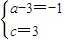 ,
,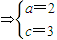
∴M=
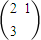 ,
,(2)∴
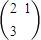
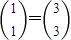 ,即点Q的坐标(3,3).
,即点Q的坐标(3,3).点评:本题考查待定系数法求矩阵,考查特征值与特征向量,理解特征值、特征向量的定义是关键.

练习册系列答案
相关题目
 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘 ,变到点
,变到点 .
. 在变换
在变换 的极坐标方程为:
的极坐标方程为: ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数).
为参数). ,曲线
,曲线 的值.
的值. 为实数,且
为实数,且

 .
. 为参数),C2的参数方程为
为参数),C2的参数方程为 为参数)
为参数) 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围. 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘 ,纵坐标乘
,纵坐标乘 ,变到点
,变到点 .
. 在变换
在变换 的极坐标方程为:
的极坐标方程为: ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数).
为参数). ,曲线
,曲线 的值.
的值. 为实数,且
为实数,且
