题目内容
已知椭圆
=1双曲线
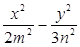＝1有公共的焦点，那么双曲线的渐近线方程是（ ）
A．x＝± | B．y＝± | C．x＝± | D．y＝± |
D
解析试题分析：由双曲线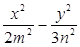＝1方程可知焦点均在x轴上，椭圆=1中
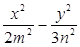双曲线＝1中
，双曲线的渐近线为
考点：椭圆双曲线的焦点渐近线性质
点评：本题的关键是先由双曲线方程确定焦点位置
练习册系列答案
名校课堂系列答案
相关题目
设
，则双曲线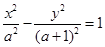
的离心率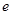
的取值范围是 （ ）
A． | B． | C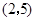． | D． |
抛物线
的焦点坐标与准线方程( )
A．焦点: ,准线: | B．焦点:,准线: |
C．焦点: , 准线: | D．焦点:, 准线: |
双曲线
（p>0）的左焦点在抛物线y2＝2px的准线上，则该双曲线的离
心率（ ）
| A．1 | B． | C． | D．2 |
已知抛物线
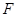上的焦点
，点
在抛物线上，点
，则要使
的值最小的点的坐标为
A． | B． | C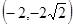． | D． |
k为何值时，直线y=kx+2和椭圆
有两个交点 （ ）
A．— <k< | B．k>或k< — |
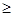C．— k | D．k 或k — |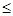
下列双曲线，离心率
的是（ ）
A． | B． |
C． | D． |
的离心率为
，且它的一条准线与抛物
的准线重合，则此双曲线的方程是( )
过抛物线
上一定点
，作两条直线分别交抛物线于
、
．当
与
的斜率存在且倾斜角互补时，则
的值为（ ）
A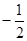． | B． | C． | D．无法确定 |