题目内容
设数列{an}的前n项和为Sn,且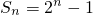 .数列{bn}满足b1=2,bn+1-2bn=8an.
.数列{bn}满足b1=2,bn+1-2bn=8an.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:数列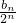 为等差数列,并求{bn}的通项公式;
为等差数列,并求{bn}的通项公式;
(Ⅲ)设数列{bn}的前n项和为Tn,是否存在常数λ,使得不等式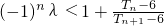 (n∈N*)恒成立?若存在,求出λ的取值范围;若不存在,请说明理由.
(n∈N*)恒成立?若存在,求出λ的取值范围;若不存在,请说明理由.
(Ⅰ)解:当n=1时 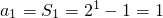 ;
;
当n≥2时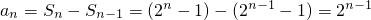 ,
,
因为a1=1适合通项公式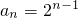 .
.
所以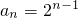 (n∈N*). …(5分)
(n∈N*). …(5分)
(Ⅱ)证明:因为 bn+1-2bn=8an,所以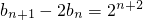 ,即
,即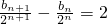 .
.
所以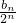 是首项为
是首项为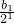 =1,公差为2的等差数列.
=1,公差为2的等差数列.
所以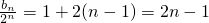 ,
,
所以 . …(9分)
. …(9分)
(Ⅲ)解:存在常数λ使得不等式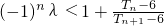 (n∈N*)恒成立.
(n∈N*)恒成立.
因为 ①
①
所以2Tn=1•22+3•23+…+(2n-5)•2n-1+(2n-3)•2n+(2n-1)•2n+1②
由①-②得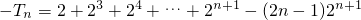 ,
,
化简得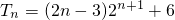 .
.
因为 =
=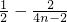 =
=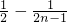 ,
,
(1)当n为奇数时,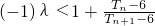 ,所以
,所以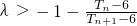 ,即
,即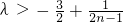 .
.
所以当n=1时,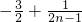 的最大值为
的最大值为 ,所以只需
,所以只需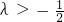 ;
;
(2)当n为偶数时,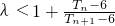 ,所以
,所以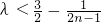 ,
,
所以当n=2时,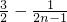 的最小值为
的最小值为 ,所以只需
,所以只需 ;
;
由(1)(2)可知存在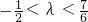 ,使得不等式
,使得不等式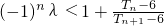 (n∈N*)恒成立.…(13分)
(n∈N*)恒成立.…(13分)
分析:(Ⅰ)根据数列递推式,再写一式,两式相减,即可求得数列{an}的通项公式;
(Ⅱ)根据bn+1-2bn=8an,可得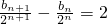 ,从而可得
,从而可得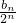 是首项为
是首项为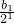 =1,公差为2的等差数列,由此可求{bn}的通项公式;
=1,公差为2的等差数列,由此可求{bn}的通项公式;
(Ⅲ)存在常数λ使得不等式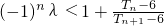 (n∈N*)恒成立.利用错位相减法求数列的和,再分类讨论,利用分离参数法,即可得到结论.
(n∈N*)恒成立.利用错位相减法求数列的和,再分类讨论,利用分离参数法,即可得到结论.
点评:本题考查数列的通项,考查等差数列的证明,考查数列的求和,考查存在性问题的探究,考查分离参数法的运用,属于中档题.
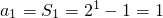 ;
;当n≥2时
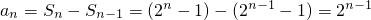 ,
,因为a1=1适合通项公式
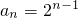 .
.所以
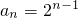 (n∈N*). …(5分)
(n∈N*). …(5分)(Ⅱ)证明:因为 bn+1-2bn=8an,所以
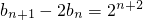 ,即
,即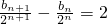 .
.所以
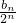 是首项为
是首项为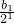 =1,公差为2的等差数列.
=1,公差为2的等差数列.所以
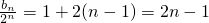 ,
,所以
 . …(9分)
. …(9分)(Ⅲ)解:存在常数λ使得不等式
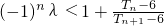 (n∈N*)恒成立.
(n∈N*)恒成立.因为
 ①
①所以2Tn=1•22+3•23+…+(2n-5)•2n-1+(2n-3)•2n+(2n-1)•2n+1②
由①-②得
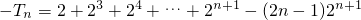 ,
,化简得
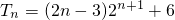 .
.因为
 =
=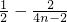 =
=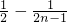 ,
,(1)当n为奇数时,
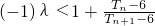 ,所以
,所以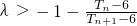 ,即
,即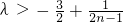 .
.所以当n=1时,
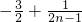 的最大值为
的最大值为 ,所以只需
,所以只需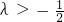 ;
;(2)当n为偶数时,
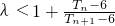 ,所以
,所以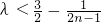 ,
,所以当n=2时,
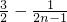 的最小值为
的最小值为 ,所以只需
,所以只需 ;
;由(1)(2)可知存在
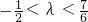 ,使得不等式
,使得不等式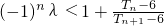 (n∈N*)恒成立.…(13分)
(n∈N*)恒成立.…(13分)分析:(Ⅰ)根据数列递推式,再写一式,两式相减,即可求得数列{an}的通项公式;
(Ⅱ)根据bn+1-2bn=8an,可得
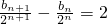 ,从而可得
,从而可得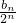 是首项为
是首项为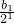 =1,公差为2的等差数列,由此可求{bn}的通项公式;
=1,公差为2的等差数列,由此可求{bn}的通项公式;(Ⅲ)存在常数λ使得不等式
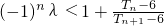 (n∈N*)恒成立.利用错位相减法求数列的和,再分类讨论,利用分离参数法,即可得到结论.
(n∈N*)恒成立.利用错位相减法求数列的和,再分类讨论,利用分离参数法,即可得到结论.点评:本题考查数列的通项,考查等差数列的证明,考查数列的求和,考查存在性问题的探究,考查分离参数法的运用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目