题目内容
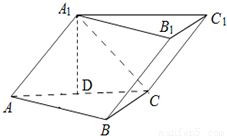
如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直, ,
,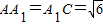 .
.(Ⅰ) 设AC的中点为D,证明A1D⊥底面ABC;
(Ⅱ) 求异面直线A1C与AB成角的余弦值.
【答案】分析:(Ⅰ)利用平面A1ACC1⊥平面ABC,可证A1D⊥底面ABC;
(Ⅱ)过B作AC的垂线BE,垂足为E,以D为原点,A1D所在直线为x轴,DC所在直线为y轴,平行于BE的直线为x轴,建立空间直角坐标系,通过计算求出向量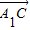 ,
, 的坐标,利用向量的夹角公式即可求得.
的坐标,利用向量的夹角公式即可求得.
解答:(Ⅰ)证明:∵AC=2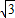 ,AA1=A1C=
,AA1=A1C=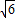 ,∴AC2=AA12+A1C2,
,∴AC2=AA12+A1C2,
∴△AA1C是等腰直角三角形,
又D是斜边AC的中点,∴A1D⊥AC,
∵平面A1ACC1⊥平面ABC,∴A1D⊥底面ABC;
(Ⅱ)∵BC=2,AC=2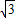 ,AB=2
,AB=2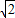 ,AC2=AB2+BC2,
,AC2=AB2+BC2,
∴三角形ABC是直角三角形,过B作AC的垂线BE,垂足为E,
则BE= =
=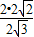 =
=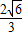 ,EC=
,EC=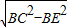 =
=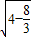 =
=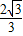 ,
,
∴DE=CD-EC=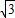 -
-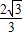 =
=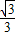 ,
,
以D为原点,A1D所在直线为x轴,DC所在直线为y轴,平行于BE的直线为x轴,建立空间直角坐标系,如图所示:
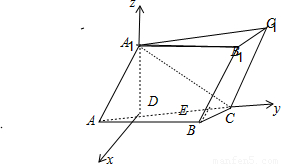
则A(0,-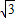 ,0),A1(0,0,
,0),A1(0,0,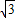 ),B(
),B(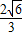 ,
,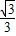 ,0),C(0,
,0),C(0, ,0),
,0),
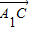 =(0,
=(0, ,-
,-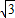 ),
),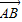 =(
=(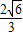 ,
,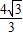 ,0),
,0),
所以cos< ,
,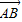 >=
>=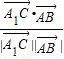 =
=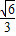 ,
,
故所求余弦值为 .
.
点评:本题考查空间中直线与平面所成的角、异面直线所成的角,考查空间向量在立体几何中的应用,考查学生的计算能力.
(Ⅱ)过B作AC的垂线BE,垂足为E,以D为原点,A1D所在直线为x轴,DC所在直线为y轴,平行于BE的直线为x轴,建立空间直角坐标系,通过计算求出向量
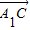 ,
, 的坐标,利用向量的夹角公式即可求得.
的坐标,利用向量的夹角公式即可求得.解答:(Ⅰ)证明:∵AC=2
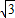 ,AA1=A1C=
,AA1=A1C=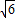 ,∴AC2=AA12+A1C2,
,∴AC2=AA12+A1C2,∴△AA1C是等腰直角三角形,
又D是斜边AC的中点,∴A1D⊥AC,
∵平面A1ACC1⊥平面ABC,∴A1D⊥底面ABC;
(Ⅱ)∵BC=2,AC=2
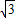 ,AB=2
,AB=2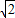 ,AC2=AB2+BC2,
,AC2=AB2+BC2,∴三角形ABC是直角三角形,过B作AC的垂线BE,垂足为E,
则BE=
 =
=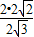 =
=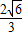 ,EC=
,EC=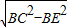 =
=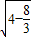 =
=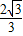 ,
,∴DE=CD-EC=
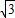 -
-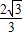 =
=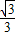 ,
,以D为原点,A1D所在直线为x轴,DC所在直线为y轴,平行于BE的直线为x轴,建立空间直角坐标系,如图所示:

则A(0,-
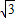 ,0),A1(0,0,
,0),A1(0,0,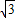 ),B(
),B(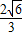 ,
,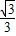 ,0),C(0,
,0),C(0, ,0),
,0),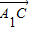 =(0,
=(0, ,-
,-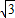 ),
),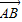 =(
=(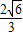 ,
,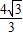 ,0),
,0),所以cos<
 ,
,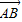 >=
>=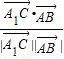 =
=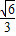 ,
,故所求余弦值为
 .
.点评:本题考查空间中直线与平面所成的角、异面直线所成的角,考查空间向量在立体几何中的应用,考查学生的计算能力.

练习册系列答案
相关题目
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.
如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.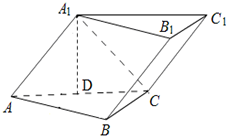 如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,
如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直, 如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.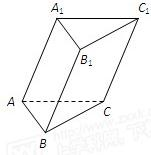 如图,已知斜三棱柱ABC-A1B1C1的底面边长分别是AB=AC=10cm,BC=12cm,侧棱AA1=13cm,顶点A1与下底面各个顶点的距离相等,求这个棱柱的全面积.
如图,已知斜三棱柱ABC-A1B1C1的底面边长分别是AB=AC=10cm,BC=12cm,侧棱AA1=13cm,顶点A1与下底面各个顶点的距离相等,求这个棱柱的全面积.