题目内容
设函数f(x)=3| x-1 |
| 2-x |
分析:由函数的解析式确定函数的定义域,再求导,求定义域内函数的极值、最值.
解答:解:函数的定义域为1≤x≤2,
f′(x)=
-
=
=0,解得x=
∴f'(x)、f(x)随x的变化如下表
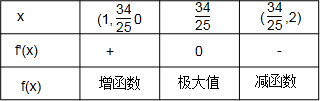
故当x=
时,函数取最大值.
f′(x)=
| 3 | ||
2
|
| 2 | ||
|
3
| ||||
2
|
| 34 |
| 25 |
∴f'(x)、f(x)随x的变化如下表

故当x=
| 34 |
| 25 |
点评:复合函数求导,函数的定义域学生易忽视.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)=
在x=1处连续,则a的值为( )
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|