题目内容
3.某几何体的三视图如图所示,则这个几何体的表面积为( )
| A. | 9 | B. | 18+9$\sqrt{3}$ | C. | 18+3$\sqrt{2}$ | D. | 9+18$\sqrt{2}$ |
分析 根据几何体的三视图,得出该几何体是底面为等腰三角形,侧棱PB⊥底面ABC的三棱锥,结合图形,求出它的表面积.
解答 解:根据几何体的三视图,得;
该几何体是底面是等腰三角形,侧棱PB⊥底面ABC的三棱锥,如图所示;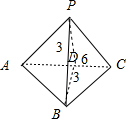
且AC=6,PB=3;
取AC的中点D,连接PD,BD,
∴BD⊥AC,BD=3;
∴S△ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×3=9,
S△PAB=S△PBC=$\frac{1}{2}$AB•PB=$\frac{1}{2}$×$\sqrt{{3}^{2}{+3}^{2}}$×3=$\frac{9}{2}$$\sqrt{2}$,
S△PAC=$\frac{1}{2}$AC•PD=$\frac{1}{2}$×6×$\sqrt{{3}^{2}{+3}^{2}}$=9$\sqrt{2}$,
∴该几何体的表面积为
S=S△ABC+S△PAD+S△PBC+S△PAC=9+$\frac{9}{2}$$\sqrt{2}$+$\frac{9}{2}$$\sqrt{2}$+9$\sqrt{2}$=9+18$\sqrt{2}$.
故选:D.
点评 本题考查了空间几何体的三视图的应用问题,解题时应根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
14.不等式4x2-4x+1>0的解集是( )
| A. | {x|x$>\frac{1}{2}$} | B. | {x|x≠$\frac{1}{2}$} | C. | R | D. | ∅ |
8.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,0<x≤16}\\{cos\frac{πx}{6},x>16}\end{array}\right.$,则f(f(-32))=( )
| A. | -1 | B. | -1+log2$\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$log23 |
 在如图所示的几何体中,四边形ABCD为平行四边形,平面AEC⊥平面ABCD,∠ACB=90°,EF∥BC,EF=$\frac{1}{2}$BC,AC=BC=2,AE=EC.
在如图所示的几何体中,四边形ABCD为平行四边形,平面AEC⊥平面ABCD,∠ACB=90°,EF∥BC,EF=$\frac{1}{2}$BC,AC=BC=2,AE=EC.