题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的定义域为
的定义域为![]() ,且满足如下两个条件:①
,且满足如下两个条件:①![]() 在
在![]() 内是单调递增函数;②存在
内是单调递增函数;②存在![]() ,使得
,使得![]() 在
在![]() 上的值域为
上的值域为![]() ,那么就称函数
,那么就称函数![]() 为“希望函数”,若函数
为“希望函数”,若函数![]() 是“希望函数”,求实数
是“希望函数”,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由函数![]() 的定义域为
的定义域为![]() ,即
,即![]() 恒成立,结合指数函数的性质,即可求解;
恒成立,结合指数函数的性质,即可求解;
(2)根据题设得到函数![]() 在
在![]() 上的值域为
上的值域为![]() ,且函数是单调递增函数,由对数函数的性质,得到
,且函数是单调递增函数,由对数函数的性质,得到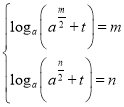 ,转化为
,转化为![]() 是
是![]() 的两个根,结合二次函数的性质,即可求解.
的两个根,结合二次函数的性质,即可求解.
(1)由题意,函数![]() 的定义域为
的定义域为![]() ,即
,即![]() 恒成立,
恒成立,
所以![]() 恒成立,因为
恒成立,因为![]() ,所以
,所以![]() ,所以
,所以![]() 的取值范围
的取值范围![]() .
.
(2)因为函数![]() 是“希望函数”,
是“希望函数”,
所以![]() 在
在![]() 上的值域为
上的值域为![]() ,且函数是单调递增函数,
,且函数是单调递增函数,
所以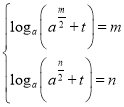 ,即
,即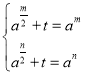 ,所以
,所以![]() 是
是![]() 的两个根,
的两个根,
设![]() ,
,
因为![]() ,所以
,所以![]() 有2个不等的正实数根,
有2个不等的正实数根,
所以![]() 且两根之积等于
且两根之积等于![]() ,解得
,解得![]()
所以实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
【题目】《中华人民共和国个人所得税法》第十四条中有下表(部分):
个人所得税税率(工资、薪金所得适用)
级数 | 全月应纳所得额 | 税率(%) |
1 | 不超过 |
|
2 | 超过 |
|
3 | 超过 |
|
4 | 超过 |
|
5 | 超过 |
|
上表中“全月应纳税所得额”是从月工资、薪金收入中减去![]() 元后的余额.如果某人月工资、薪金收入为
元后的余额.如果某人月工资、薪金收入为![]() 元,那么他应纳的个人所得税为________元.
元,那么他应纳的个人所得税为________元.
