题目内容
【题目】已知等差数列{an}的前n项和为Sn ， 公差d≠0，S5=4a3+6，且a1 ， a3 ， a9成等比数列．
（1）求数列{an}的通项公式；
（2）求数列{ 
}的前n项和公式．
【答案】
（1）解：因为S5=4a3+6，所以5a1+10d=4（a1+2d）+6．①
因为a1，a3，a9成等比数列，所以a1（a1+8d）=（a1+2d）2．②
由①②及d≠0可得：a1=2，d=2．
所以an=2n
（2）解：由an=2n，可知Sn=n2+n
所以 
= 
= 
，
所以数列{ }的前n项和为1﹣ 
+ ﹣ 
+…+ = 
= 
【解析】（1）利用S5=4a3+6a，且a1 ， a3 ， a9成等比数列，建立方程，可求数列的首项与公差，即可得到数列{an}的通项公式；（2）利用裂项法，即可求数列{ }的前n项和公式．
【考点精析】认真审题，首先需要了解等差数列的通项公式（及其变式）(通项公式：
或
)，还要掌握等比数列的通项公式（及其变式）(通项公式：
)的相关知识才是答题的关键．
一线名师权威作业本系列答案
【题目】为了培养学生的安全意识，某中学举行了一次安全自救的知识竞赛活动，共有800 名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100 分）进行统计，得到如下的频率分布表，请你根据频率分布表解答下列问题：
序号 | 分组 | 组中值 | 频数 | 频率 |
1 | [60，70） | 65 | ① | 0.10 |
2 | [70，80） | 75 | 20 | ② |
3 | [80，90） | 85 | ③ | 0.20 |
4 | [90，100） | 95 | ④ | ⑤ |
合计 | 50 | 1 | ||
（1）求出频率分布表中①、②、③、④、⑤的值；
（2）为鼓励更多的学生了解“安全自救”知识，成绩不低于85分的学生能获奖，请估计在参加的800名学生中大约有多少名学生获奖？
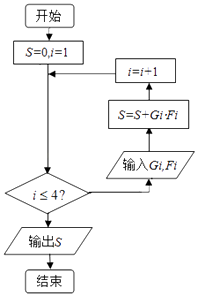
（3）在上述统计数据的分析中，有一项指标计算的程序框图如图所示，则该程序的功能是什么？求输出的S的值．
