Question

符号[x]表示不超过x的最大整数，如[2]=2，[π]=3，[-

2

]=-2，定义函数f（x）=x-[x]，设函数g（x）=-

x

3

，若f（x）在区间x∈（0，2）上零点的个数记为a，f（x）与g（x）图象交点的个数记为b，则

∫

b a

 g(x)dx的值是

-

5

2

．

Answer 1

分析：先画出f（x）=x-[x]的图象，根据图象得出f（x）在区间x∈（0，2）上零点的个数以及f（x）与g（x）=-

x

3

图象交点的个数，求出a和b的值得到积分上下限，再根据定积分的运算法则求解即可．

解答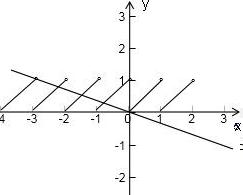：解：画出函数f（x）=x-[x]的图象．
由图象可知若f（x）在区间x∈（0，2）上零点的个数为a=1，
f（x）与g（x）=-

x

3

图象交点的个数为b=4，

∫

b a

 g(x)dx=∫₁⁴（-

x

3

）dx=（-

x2

6

）|₁⁴=-

5

2

，
故答案为：-

5

2

．

点评：本题主要考查了函数的零点、定积分的运算，考查运算求解能力，考查数形结合思想，属于基础题．