题目内容
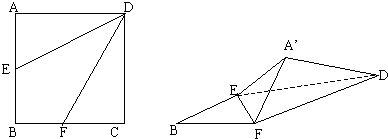 (2003•海淀区一模)正方形ABCD中,AB=2,E、F分别是边AB及BC的中点,将△AED及△DCF折起(如图),使A、C点重合于A′点,
(2003•海淀区一模)正方形ABCD中,AB=2,E、F分别是边AB及BC的中点,将△AED及△DCF折起(如图),使A、C点重合于A′点,(Ⅰ)证明:A′D⊥EF;
(Ⅱ)求三棱锥A′-EFD的体积;
(Ⅲ)求A′D与平面DEF所成角的正切值.
分析:(Ⅰ)利用线面垂直的性质证明AD⊥EF;
(Ⅱ)利用等积法求三棱锥A-EFD的体积;
(Ⅲ)利用直线和平面所成角的定义求值.
(Ⅱ)利用等积法求三棱锥A-EFD的体积;
(Ⅲ)利用直线和平面所成角的定义求值.
解答:证明:(I)∵A′D⊥A′E,A′D⊥A′F,
∴A′D⊥平面A′EF,
∴A′D⊥EF…(4分)
(II)∵A′D⊥平面A′EF,
∴A′D的长为三棱锥D-A′EF的高
∵A′E=A′F=1,EF=
,
∴∠EA′F=90°…(6分)
∴VA′-EFD=VD-A′EF=
S△A′EF•DA′=
•
•2=
…(9分)
(III)取EF中点G,连A′G,DG,∵A′E=A′F=1,∠EA′F=90°,
∴A′G⊥EF且A′G=
.
又∵A′D⊥EF∴EF⊥平面A′DG,
∴平面DEF⊥平面A′DG…(11分)
作A′H⊥DG于H,得A′H⊥平面DEF,
∴∠A′DG为A′D与平面DEF所成角…(14分)
在直角三角形A′DG中,A′G=
.A'D=2,
∴tanA′DG=
…(16分)
∴A′D⊥平面A′EF,
∴A′D⊥EF…(4分)
(II)∵A′D⊥平面A′EF,
∴A′D的长为三棱锥D-A′EF的高
∵A′E=A′F=1,EF=
| 2 |
∴∠EA′F=90°…(6分)
∴VA′-EFD=VD-A′EF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(III)取EF中点G,连A′G,DG,∵A′E=A′F=1,∠EA′F=90°,
∴A′G⊥EF且A′G=
| ||
| 2 |
又∵A′D⊥EF∴EF⊥平面A′DG,
∴平面DEF⊥平面A′DG…(11分)
作A′H⊥DG于H,得A′H⊥平面DEF,
∴∠A′DG为A′D与平面DEF所成角…(14分)
在直角三角形A′DG中,A′G=
| ||
| 2 |
∴tanA′DG=
| ||
| 4 |
点评:本题主要考查线面垂直的性质的应用,以及锥体的体积公式,线面角的求法,考查学生的基本运算能力.

练习册系列答案
相关题目