题目内容
在△ABC中,角A、B、C的对边分别为a,b,c,
=
.
(Ⅰ)求角B的大小;
(Ⅱ)求函数f(x)=cosx•cos(x+B)(x∈[0,
])的值域.
| tanB |
| tanC |
| 2a-c |
| c |
(Ⅰ)求角B的大小;
(Ⅱ)求函数f(x)=cosx•cos(x+B)(x∈[0,
| π |
| 2 |
(Ⅰ)∵
=
,而sinC>0
∴sinBcosC=2sinAcosB-cosBsinC,
∴sin(B+C)=2sinAcosB=sinA
∴cosB=
,∴B=
;
(Ⅱ)f(x)=
cos2x-
sinxcosx
=
-
sin2x
=
cos(2x+
)+
∵2x+
∈[
,
π],
∴-1≤cos(2x+
)≤
,
∴f(x)的值域为[-
,
].
| sinBcosC |
| sinCcosB |
| 2sinA-sinC |
| sinC |
∴sinBcosC=2sinAcosB-cosBsinC,
∴sin(B+C)=2sinAcosB=sinA
∴cosB=
| 1 |
| 2 |
| π |
| 3 |
(Ⅱ)f(x)=
| 1 |
| 2 |
| ||
| 2 |
=
| 1+cos2x |
| 4 |
| ||
| 4 |
=
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 4 |
∵2x+
| π |
| 3 |
| π |
| 3 |
| 4 |
| 3 |
∴-1≤cos(2x+
| π |
| 3 |
| 1 |
| 2 |
∴f(x)的值域为[-
| 1 |
| 4 |
| 1 |
| 2 |

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
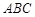 的面积是
的面积是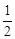 ,
,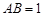 ,
,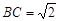 ,则
,则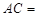 ( )
( )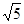
 中,内角
中,内角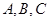 所对的边分别为
所对的边分别为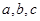 .已知
.已知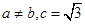 ,
,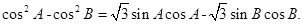
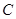 的大小;
的大小;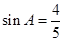 ,求
,求