Question

已知A、B、C三点在球心为O，半径为3的球面上，且几何体O-ABC为正三棱锥，若A、B两点的球面距离为π，则正三棱锥的侧面与底面所成角的余弦值为    ．

Answer 1

【答案】分析：欲求正三棱锥的侧面与底面所成角的余弦值，先求出A、B两点的球心角∠AOB，再利用题设条件求出几何体O-ABC为正四面体，利用余弦定理即得．
解答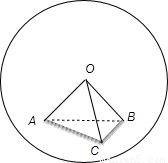：解：作出图形，
∵A、B两点的球面距离为π，
∴球心角∠AOB=，
∵OA=OB=3，∴AB=3．
∵几何体O-ABC为正三棱锥，∴几何体O-ABC为正四面体，
设正四面体O-ABC的棱长为2，取AC中点D，连接OD，BD，
∵OA=OC=AC=AB=BC=2，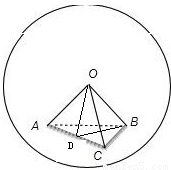
∴OD⊥AC，BD⊥AC，OD=BD=，
∴∠ODB是正三棱锥的侧面与底面所成角，
∴cos∠ODB==．
故答案为：．
点评：本题主要考查了点、线、面间的距离计算，考查空间想象能力、运算能力和推理论证能力，属于中档题．解题时要注意余弦定理的灵活运用．