题目内容
已知A,B,C三点在球心为O,半径为3的球面上,且几何体O-ABC为正四面体,那么A,B两点的球面距离为分析:欲求A,B两点的球面距离,先求出A、B两点的球心角∠AOB,再利用球面距离的定义即可求出,将点O到平面ABC的距离转化为点O到直线AD的距离,通过解直角三角形即得.
解答:解:作出图形,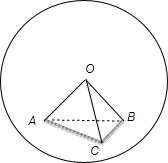
∵几何体O-ABC为正四面体,
∴球心角∠AOB=
∴A,B两点的球面距离=
×3=π.
∵几何体O-ABC为正四面体,
∴球心在平面ABC上的射影是三角形的中心Q,
∴点O到平面ABC的距离为OQ,
在直角三角形OAQ中,
OA=3,AQ=
AD=
,
∴OQ=
=
.
故答案为:π,

∵几何体O-ABC为正四面体,
∴球心角∠AOB=
| π |
| 3 |
∴A,B两点的球面距离=
| π |
| 3 |
∵几何体O-ABC为正四面体,
∴球心在平面ABC上的射影是三角形的中心Q,
∴点O到平面ABC的距离为OQ,
在直角三角形OAQ中,
OA=3,AQ=
| 2 |
| 3 |
| 3 |
∴OQ=
| 9-3 |
| 6 |
故答案为:π,
| 6 |
点评:本题主要考查了点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目