题目内容
已知A，B，C三点在球心为O，半径为3的球面上，且几何体O-ABC为正四面体，那么A，B两点的球面距离为分析：欲求A，B两点的球面距离，先求出A、B两点的球心角∠AOB，再利用球面距离的定义即可求出．
解答：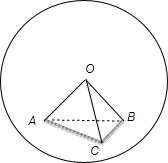
解：作出图形，
∵几何体O-ABC为正四面体，
∴球心角∠AOB=
∴A，B两点的球面距离=
×3=π．
故填：π
解：作出图形，∵几何体O-ABC为正四面体，
∴球心角∠AOB=
| π |
| 3 |
∴A，B两点的球面距离=
| π |
| 3 |
故填：π
点评：本题主要考查了球内接多面体及球面距离的求法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目