题目内容
已知A(1,2),B(0,1),C(1,1)则
与
的夹角的余弦值为( )
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:由题意易得两向量的坐标,由夹角公式可得.
解答:
解:∵A(1,2),B(0,1),C(1,1),
∴
=(-1,-1),
=(0,-1),
∴|
|=
=
,|
|=1,
•
=-1×0+(-1)×(-1)=1,
∴
与
的夹角的余弦值为
=
=
故选:B
∴
| AB |
| AC |
∴|
| AB |
| (-1)2+(-1)2 |
| 2 |
| AC |
| AB |
| AC |
∴
| AB |
| AC |
| ||||
|
|
| 1 | ||
|
| ||
| 2 |
故选:B
点评:本题考查数量积与向量的夹角,属基础题.

练习册系列答案
相关题目
对两条不相交的空间直线a与b,必存在平面α,使得( )
| A、a?α,b?α |
| B、a?α,b∥α |
| C、a⊥α,b⊥α |
| D、a?α,b⊥α |
命题“若x2<1,则-1<x<1”的逆否命题是( )
| A、若x2≥1,则x≥1且x≤-1 |
| B、若-1<x<1,则x2<1 |
| C、若x>1或x<-1,则x2>1 |
| D、若x≥1或x≤-1,则x2≥1 |
有四个数a1,a2,a3,a4,前三个数成等比,积为64;后三个数成等差,和为6;则a1=( )
| A、9 | B、8 | C、16 | D、4 |
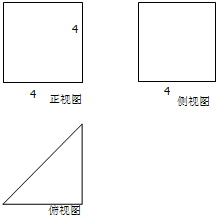 一个几何体的三视图如图所示,则这个几何体的表面积等于
一个几何体的三视图如图所示,则这个几何体的表面积等于