题目内容
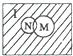 设全集I是实数集R,M={x|x2>4}与N={x|
设全集I是实数集R,M={x|x2>4}与N={x|| 2 |
| x-1 |
| A、{x|-2≤x<1} |
| B、{x|-2≤x≤1} |
| C、{x|-2<x≤1} |
| D、{x|x<2} |
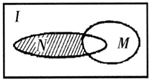
分析:根据Venn图表达集合的关系我们易判断阴影部(如图所示)所表示的集合为CI(M∪N),解不等式我们易求出集合M,N代入即可求出阴影部分所表示的集合.
解答:解:由图可知图中阴影部分的面积表示的集合为CI(M∪N)
∵M=x|x2>4=(-∞,-2)∪(2,+∞)
N={x|
≥1}=(1,3]
∴M∪N=(-∞,-2)∪(1,+∞)
∴CI(M∪N)=[-2,1]
故选B
∵M=x|x2>4=(-∞,-2)∪(2,+∞)
N={x|
| 2 |
| x-1 |
∴M∪N=(-∞,-2)∪(1,+∞)
∴CI(M∪N)=[-2,1]
故选B
点评:本题考查的知识点是Venn图表达集合的关系及运算,二次不等式的解法,分式不等式的解法,其中根据Venn图表达集合的关系我们易判断阴影部(如图所示)所表示的集合是解答本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 设全集I是实数集R,M={x|x>2}与N={x|
设全集I是实数集R,M={x|x>2}与N={x|| x-3 |
| x-1 |
| A、{x|1<x≤2} |
| B、{x|-2≤x<1} |
| C、{x|x<2} |
| D、{x|-2≤x≤2} |
 1、设全集I是实数集R,M={x|x2>4}与N={x|1<x≤3}都是I的子集(如图所示),则阴影部分所表示的集合为( )
1、设全集I是实数集R,M={x|x2>4}与N={x|1<x≤3}都是I的子集(如图所示),则阴影部分所表示的集合为( ) 设全集I是实数集R,M=(-1,0]∪(2,+∞)与N=(-2,2)都是I的子集,则右图阴影部分所表示的集合为
设全集I是实数集R,M=(-1,0]∪(2,+∞)与N=(-2,2)都是I的子集,则右图阴影部分所表示的集合为