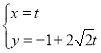题目内容
【题目】已知数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() 为递增数列,且
为递增数列,且![]() 成等差数列,求
成等差数列,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() 是递增数列,
是递增数列,![]() 是递减数列,求数列
是递减数列,求数列![]() 的通项公式.
的通项公式.
【答案】(1)![]() (2)
(2)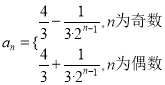 或
或![]()
【解析】
试题分析:(1)利用数列![]() 的单调性,得到
的单调性,得到![]() 的符号去掉
的符号去掉![]() 的绝对值,再分布令
的绝对值,再分布令![]() 得到
得到![]() 之间的关系,再利用题目已知等差中项的性质列出关于
之间的关系,再利用题目已知等差中项的性质列出关于![]() 的等式,即可求出
的等式,即可求出![]() 的值.
的值.
(2)根据数列![]() 在
在![]() 为奇数和偶数的单调性可得到
为奇数和偶数的单调性可得到![]() 且
且![]() ,两不等式变为同号相加即可得到
,两不等式变为同号相加即可得到![]() ,根据题意可得
,根据题意可得![]() 结合
结合![]() 与
与![]() 可去掉
可去掉![]() 的绝对值,分
的绝对值,分![]() 为奇或偶数,利用叠加法即可求出数列
为奇或偶数,利用叠加法即可求出数列![]() 的通项公式.
的通项公式.
(1)因为数列![]() 为递增数列,所以
为递增数列,所以![]() ,则
,则![]() ,分别令
,分别令![]() 可得
可得![]()
![]() ,因为
,因为![]() 成等差数列,所以
成等差数列,所以![]()
![]()
![]() 或
或![]() ,
,
当![]() 时,数列
时,数列![]() 为常数数列不符合数列
为常数数列不符合数列![]() 是递增数列,所以
是递增数列,所以![]() .
.
(2)由题可得![]() ,因为
,因为![]() 是递增数列且
是递增数列且![]() 是递减数列,所以
是递减数列,所以![]() 且
且![]()
![]() ,两不等式相加可得
,两不等式相加可得![]()
![]() ,
,
又因为![]()
![]() ,所以
,所以![]() ,即
,即![]() ,
,
同理可得![]() 且
且![]() ,所以
,所以![]() ,
,
则当![]()
![]() 时,
时,![]() ,这
,这![]() 个等式相加可得
个等式相加可得![]()
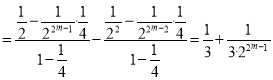
![]() .
.
当![]() 时,
时,![]() ,这
,这![]() 个等式相加可得
个等式相加可得![]()
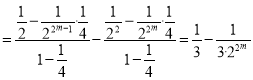
![]() ,当
,当![]() 时,
时,![]() 符合,故
符合,故![]()
综上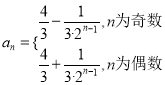 .
.

【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: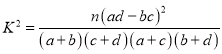 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
【题目】某公司新研发了一款手机应用APP,投入市场三个月后,公司对部分用户做了调研:抽取了400位使用者,每人填写一份综合评分表(满分为100分).现从400份评分表中,随机抽取40份(其中男、女使用者的评分表各20份)作为样本,经统计得到如下的茎叶图:
女性使用者评分 | 男性使用者评分 | |
7 | 6 | 7 8 9 9 |
1 2 5 | 7 | 0 2 2 3 4 5 6 6 7 8 9 |
0 3 3 3 4 4 5 6 6 8 | 8 | 2 4 4 9 |
0 0 1 2 2 2 | 9 | 2 |
记该样本的中位数为![]() ,按评分情况将使用者对该APP的态度分为三种类型:评分不小于
,按评分情况将使用者对该APP的态度分为三种类型:评分不小于![]() 的称为“满意型”,评分不大于
的称为“满意型”,评分不大于![]() 的称为“不满意型”,其余的都称为“须改进型”.
的称为“不满意型”,其余的都称为“须改进型”.
(1)求![]() 的值,并估计这400名使用者中“须改进型”使用者的个数;
的值,并估计这400名使用者中“须改进型”使用者的个数;
(2)为了改进服务,公司对“不满意型”使用者进行了回访,根据回访意见改进后,再从“不满意型”使用者中随机抽取3人进行第二次调查,记这3人中的女性使用者人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.